1. 서 론
2. 이론적 배경
2.1 Exponential Smoothing(ETS)
2.2 Auto-Regressive Integratdf Moving Average(ARIMA)
3. 적용 및 결과
3.1 입력 변수 설정
3.2 ETS와 ARIMA모형의 결과 비교
4. 결 론
1. 서 론
전 세계적으로 자원 고갈과 대기환경 보존을 위한 요구로 지속가능발전을 위한 교통수단의 관심과 함께 친환경자동차의 역할이 강조됨에 따라 현재 우리나라에서도 2030국가 온실가스 감축 기본 로드맵(2016), 제3차 지속가능발전 기본계획(2016), 미세먼지 관리 특별대책 세부이행계획(2016) 등의 수립을 통해 친환경자동차 보급 활성화 정책을 추진하고 있다. 특히 친환경자동차 중에서도 전기자동차를 중심으로 충전시설 확충, 전기자동차 특례 요금제, 생활 주변 충전인프라 개선 등의 사업을 통해 전기자동차 시장 활성화를 도모하고 있다. 전기자동차 시장이 안정적으로 활성화하기 위해서는 충전시설 확충에 따른 안정적인 전력 공급이 필요하며 이를 위해 전기자동차 충전으로 발생하는 전력수요예측은 매우 중요한 사항이라고 할 수 있다. 또한, 신재생 에너지 보급 확대, 수요 자원의 증가, 급격한 전력 수요 패턴 변동 및 기후변화로 인하여 전력 수요 예측의 중요성이 높아지고 있다(Kim, 2013). 전력수요예측은 예측 기간에 따라서 초단기, 단기, 중기, 장기로 구분할 수 있다. 단기 전력수요예측은 1시간에서 1주일까지의 미래 전력수요예측을 수행한다. 단기 전력수요예측의 결과는 전력 시장의 발전 가격 결정, 예비력 및 송전 용량 확보를 위한 발전기 운영 계획 등에 활용된다. 따라서 정확한 단기 전력수요 예측은 안정적인 전력 계통의 운영과 효율적인 전력시장 운영에 기여한다(Kim, 2019). 전력수요 예측 방법으로는 통계적 기법, 인공지능 기법으로 구분할 수 있다. 통계적 방법으로는 현재까지의 관측 정보, 이와 관련된 정보들 간의 수학적인 조합을 통하여 미래의 전력 수요량을 예측하는 방법이며 ETS, 시계열 분석법 등이 있다. ETS는 현재 시점에 대해 예측된 수요량과 실제 수요량의 가중 평균으로 미래의 수요량을 예측하는 방법으로 시계열 데이터의 추세와 계절성을 고려한 Holt-Winter 지수평활 모델이 대표적이다(Kim et al., 2017). 시계열 분석 모델에는 현재의 시계열이 과거의 관측 값에 영향을 받는 자기회귀모델(Autoregressive model : AR), 시계열이 과거의 오차항으로 표현되는 이동평균모델(Moving Average model : MA), AR 모델과 MA모델 을 혼합한 자기회귀이동평균 모델(Autoregressive Moving Average model : ARMA), 비정상 시계열 차분연산을 통해 정상 시계열로 변화시켜 ARMA 모델에 포함시키는 ARIMA 모델이 있다(Kim et al., 2014; Ko and Lee, 2016). 최근 컴퓨팅 기술의 발달로 인해 인공지능 기법을 다양한 영역에서 활용 중에 있다. 인공지능 기법에는 일반적으로 인공신경망, 웨이브렛 변화, 서포트 벡터머신, 하이브리드 모델 등 다양한 모델들이 존재한다. 서포트 벡터머신은 머신러닝 모델 중 하나로 패턴 인식이나 자료 분석을 위한 회귀분석, 분류를 위하여 이용하는 모델이다(Ramanarayanan et al., 1997; Yang et al., 2016). 이렇든 본 논문에서 전기자동차 충전시설의 전력수요량 예측을 위하여 전기자동차 충전에 영향을 미치는 변수를 도출 후 요인분석을 통해 변수를 선정하고 입력자료를 ETS에 적용 후 전력 수요량을 예측하고 통계적 방법인 ARIMA모형의 결과와 비교하였다. 비교 결과 ETS가 더 높은 정확도를 보였다.
2. 이론적 배경
2.1 Exponential Smoothing(ETS)
일반적인 ETS 모형은 Eq. (1)과 같이 표현된다.
단, 는 시점 에서의 총 관측값, 초기 값 는 평균 값, 는 데이터의 영향 정도를 결정하는 지수평활 상수을 의미한다.
이 방법은 값이 클수록 최근 데이터에 상대적으로 큰 가중치를 준다. 지수평활 상수 값의 결정은 0 ~ 1 사이에서 경험적으로 가장 효과적인 값을 이용한다. 이러한 ETS는 계산이 간단하고 최신자료를 많이 반영하는 적시성 때문에 많은 공학 분야에 활발히 활용되고 있다.
2.2 Auto-Regressive Integratdf Moving Average(ARIMA)
ARIMA 모형은 비정상 시계열을 차 차분하여 정상 시계열로 변환한 이후에 정상 시계열 모형을 ARMA(Auto-Regressive Moving Average)모형에 적합시킨 모형을 말한다. 시계열 가 평균인 인 ARIMA(, , ) 모형식은 Eq. (2)과 같이 표현한다.
는 시점에서의 관측값을, 는 후진 연산자(back-shift operator)를 의미한다. 는 AR 차수, 는 MA 차수이며, 는 차분 차수를 의미한다. , 는 각각 , , 차 다항식으로 각각의 식은 아래 Eqs. (3), (4)와 같다.
3. 적용 및 결과
3.1 입력 변수 설정
3.1.1 입력 변수 구축
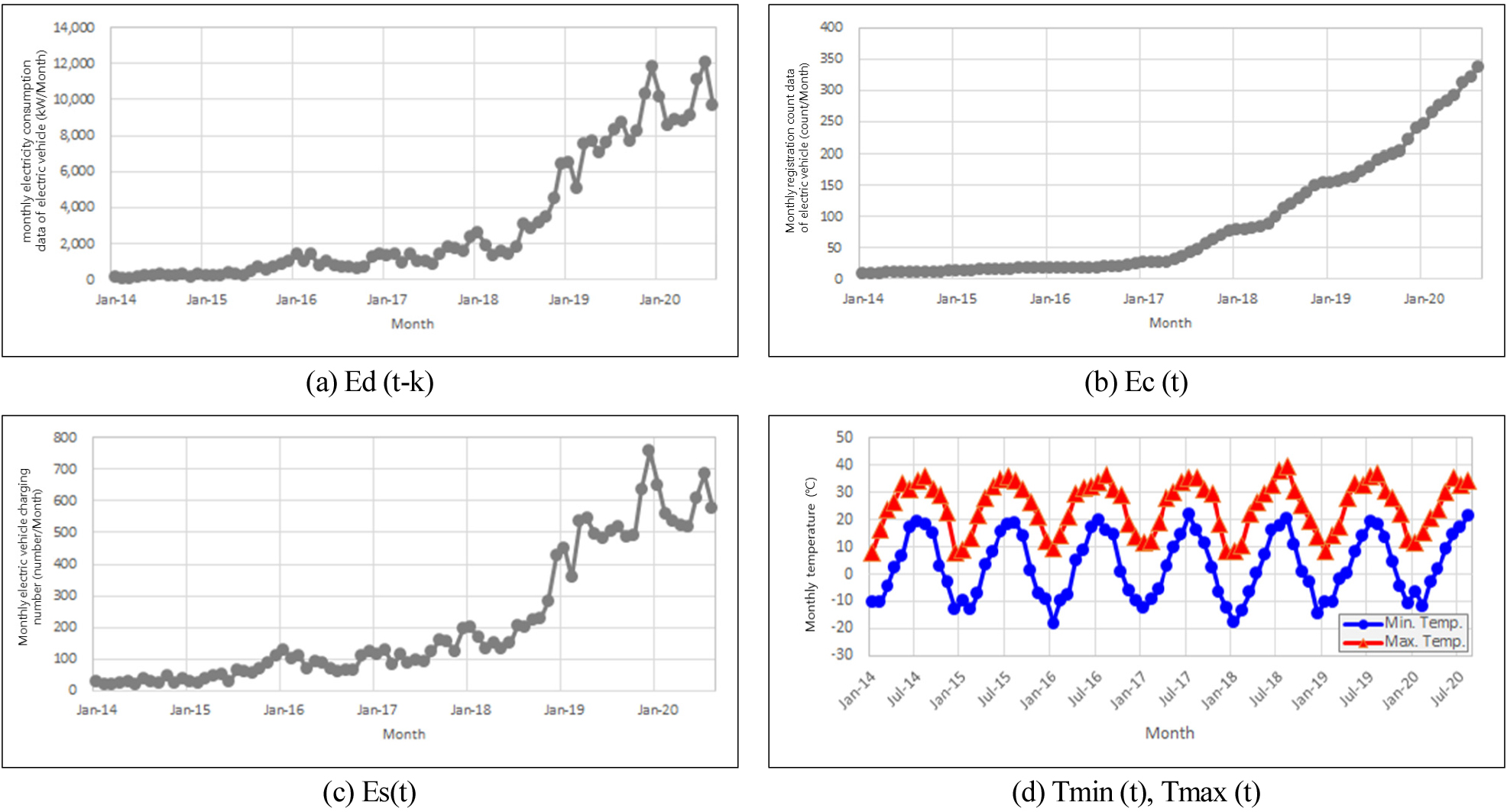
전기자동차 충전소 전력 사용량 예측을 위하여 서울특별시 종로구를 대상으로 입력데이터를 수집하여 종속변수로 월별 시군구 전력 사용량을 독립변수로 월별 시군구 충전소 보급대수, 월별 시군구 전기자동차 충전소 충전 횟수, 월별 전기자동차 등록대수 자료를 구축하였다(Table 1).
Table 1.
List of Input Variables
대상 기간은 2014년 1월부터 2020년 8월까지 자료를 수집하고 이를 통해 구축된 독립 변수별로 시계열 자료를 확인해본 결과 월별 시군구 전력 사용량, 월별 시군구 전기자동차 충전소 충전 횟수, 월별 전기자동차 등록 대수는 18년 이후로 급격히 상승하는 경향을 보이는 것으로 확인되었다(Fig. 1).
3.1.2 요인분석을 이용한 변수 선정
요인분석을 수행하기 앞서 선행되어야 할 것은 변수간 신뢰도 분석이며, 이는 각 변수를 사용하기 적합한 변수인지 통계적으로 검증하는 단계로 아래 Table 2의 신뢰도 통계량 표에서 Cronbach의 알파 값은 0.7 이상일 경우 각 자료가 높은 신뢰도를 나타낸다고 볼 수 있다.
Table 2.
Reliability Statistics By Variable
결과를 살펴보면 전력수요량, 전기자동차 공급대수, 전기자동차 충전횟수, 최저기온, 최고기온 모두 0.7 이상으로 각 변수들이 요인분석을 하기 적합한 자료임을 알 수 있다.
신뢰도 분석 후 각 변수별 상관행렬 표를 작성하고 상관행렬 표는 요인분석에 이용된 변수들 간의 상관관계를 확인한다. 이때 상관계수가 0.3보다 작아지면 요인분석에 적합하지 않은 변수이므로 제외시켜야 한다.
본 논문에서는 KMO 측도와 Barlett의 구형성 검정을 통해 각 변수들이 요인분석에 적합한 변수인지 확인하기 위해 Table 3과 같이 변수별 상관행렬을 분석하였고, Table 4와 같이 KMO와 Bartlett 검정을 수하였다. 그 결과 KMO측도가 0.64이고 Bartlett의 구형성 검정의 유의확률이 0.00으로 요인분석에 적합한 변수로 판단하였다.
Table 3.
Correlation Matrix By Variable
Table 4.
Kaiser-Meyer-Olkin (KMO) and Bartlett’s Test
| Kaiser-Meyer-Olkin Measure | Initial value | ||
| Approximate chi-square | Degree of freedom | Significance probability | |
| 0.640 | 727.7 | 10 | 0.000 |
변수들의 적합성의 평가결과 구축한 변수들이 요인분석에 적용하기 적합하다고 판단하여 총 분산표와 스크리 도표를 이용하여 요인분석을 수행하였고, 먼저 공통성(Communality)표를 통해 추출된 요인들에 의해 각 변수가 얼마나 설명되는지 확인하였다. Table 5의 총 분산표의 추출 값이 0.5보다 작을 경우, 그 변수를 무시하고 나머지 변수를 중심으로 해석하거나, 그 변수를 제거 후 요인분석을 재분석이 요구되지만, 분석결과 5개 변수 모두 0.9 이상을 나타내고 있으므로 요인분석을 계속 진행하였다.
Table 5.
Findings of Communality Analysis Through Principal Component Analysis
| Item | Ed (t-k) | Ec (t) | Es (t) | Tmin (t) | Tmax (t) |
| Initially | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Extract | 0.992 | 0.965 | 0.985 | 0.972 | 0.972 |
요인추출방법으로 주성분분석을 사용하였으며 Eigenvalue=1을 기준으로 추출하였기 때문에 총 분산 분석표(Table 6)에서 2개의 요인이 추출된 것을 확인하였고, 2개의 요인들이 전체 분산의 97.7%의 설명력을 나타내고 있으며, Fig. 2의 스크리 도표의 작성 결과 2개의 요인이 선택된 것을 확인하였다.
Table 6.
Findings of Total Variable Analysis Through Principal Component Analysis
성분분석결과 일반적으로 성분 행렬의 값이 0.4이상인 값을 사용하며, 제 1성분에서 전력수요량과 전기자동차 충전 횟수, 전기자동차 공급 대수가 0.4이상의 값을 나타내며 최고 기온과 최저 기온은 제외되는 것을 확인할 수 있다(Table 7).
Table 7.
Component Analysis
| Item | Ed (t-k) | Ec (t) | Es (t) | Tmin (t) | Tmax (t) | |
| Component | 1 | 0.996 | 0.992 | 0.981 | -0.006 | 0.031 |
| 2 | 0.006 | -0.030 | 0.060 | 0.986 | 0.985 | |
3.2 ETS와 ARIMA모형의 결과 비교
앞서 언급하였듯이 2014년 1월부터 2019년 8월까지의 자료를 학습기간으로 2019년 9월부터 2020년 8월까지를 검증기간으로 설정하였다. 또한 기존의 시계열 예측 방법인 ETS, ARIMA 결과와 비교를 통해 ETS모형의 적용성을 검토하였다.
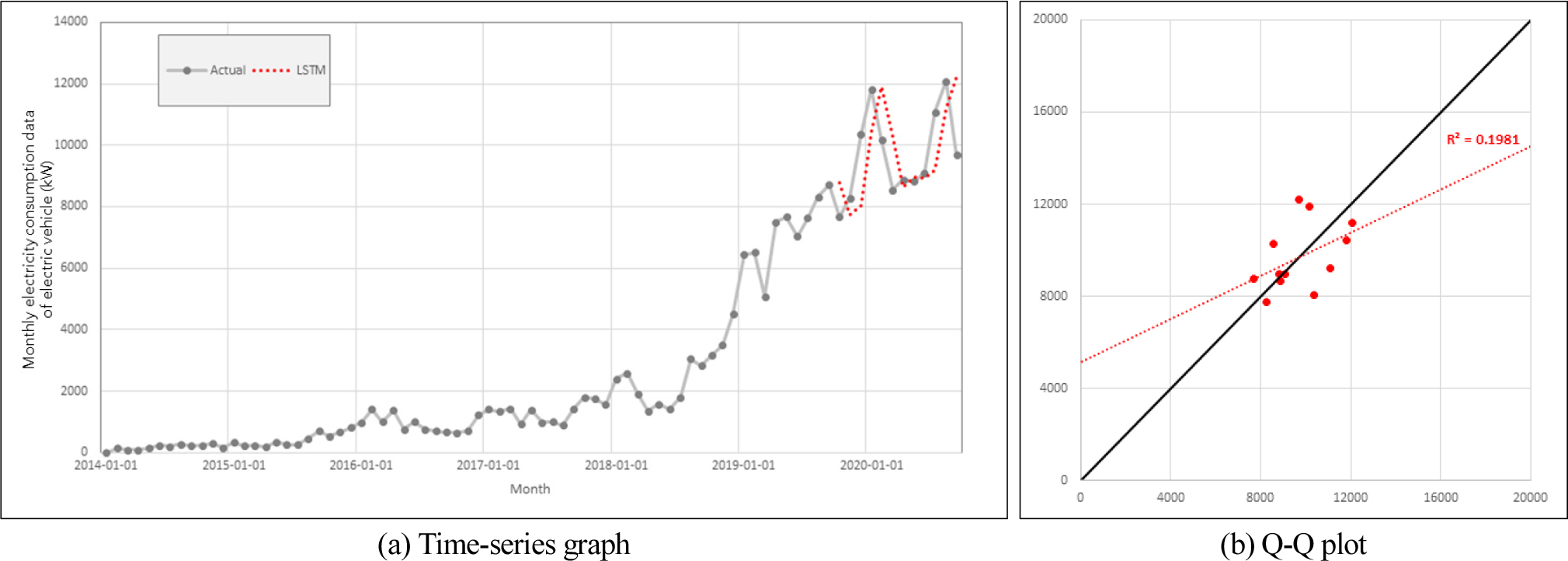
ETS를 이용하여 전기자동차 전력수요량을 검토한 결과 오차율이 12%, R2이 0.2, NSE가 -0.45로 낮은 유사도로 분석되었다(Fig. 3).
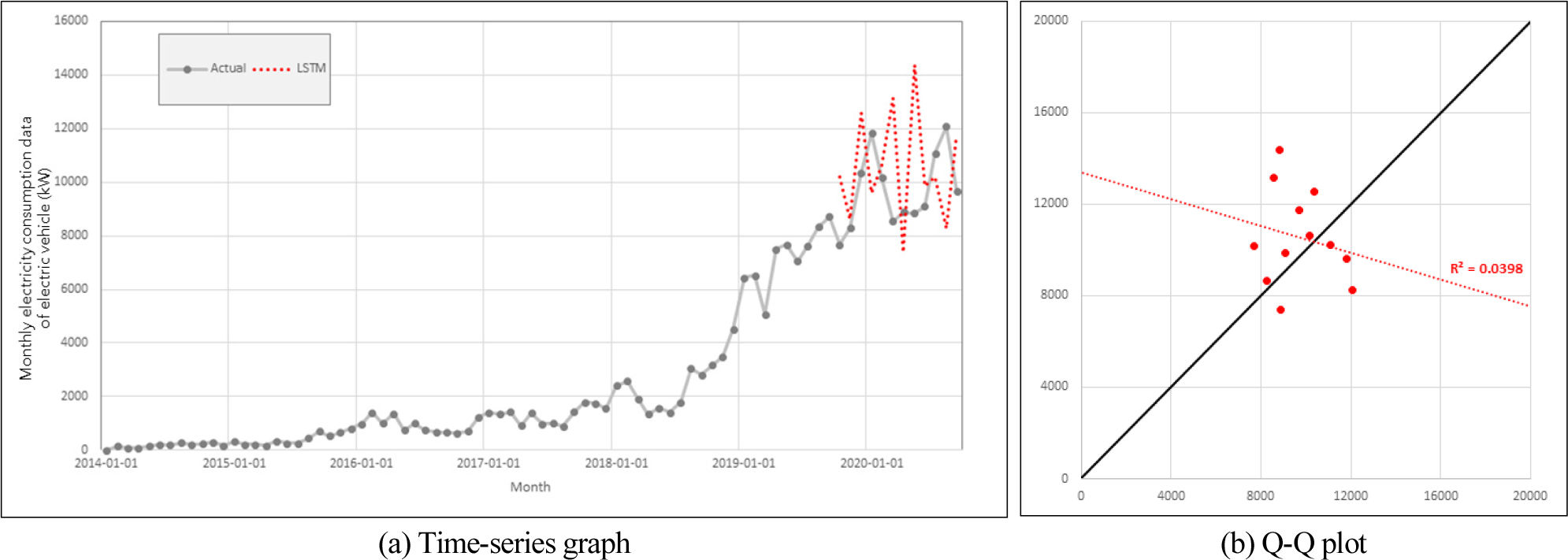
ARIMA를 이용하여 전기자동차 전력수요량을 검토한 결과 오차율이 21%, R2이 0.04, NSE가 –4.09로 낮은 유사도로 분석되었다(Fig. 4).
4. 결 론
본 논문은 전기자동차 전력 수요량을 시계열로 예측하기 위하여 ETS 기법을 적용하였고 전기자동차 전력 수요량에 영향을 미치는 변수를 도출 후 요인분석을 통해 변수를 선정하고 입력자료를 구축하였다.
입력자료는 2014년 1월부터 2020년 8월까지 월단위로 자료를 수집 후 모형의 검증을 위해 2014년 1월부터 2019년 8월까지의 자료를 학습기간으로 2019년 9월부터 2020년 8월까지를 검증기간으로 설정하였고 변수별로 정규화 하여 활용하였다.
전기자동차 전력 수요량 예측 결과의 검증을 위하여 ETS와 ARIMA를 이용하여 전기자동차 전력 수요량 예측하여 결과를 비교한 결과 ETS(오차율 12%, R² 0.04, NSE –0.45)와 ARIMA(오차율 21%, R² 0.04, NSE –4.09)로 Table 8과 같이 ETS 모형이 더 좋은 결과를 보였다. [6]는 R²와 NSE가 각각 0.5, 0.4 이상이면 모형이 실 관측값을 잘 모의하는 것으로 제안하였으며, 이에 따라 본 논문에서는 ETS를 이용한 전력 수요 예측 모형으로써의 적합성을 확인 하였다.
향후 전기자동차 전력 수요량 예측 관련 시계열데이터가 장기간에 걸쳐 수집된다면 이러한 문제는 해결될 것이며 이를 통해 보다 정확하고 장기간의 전기자동차 전력 수요량 예측을 통해 궁극적으로는 정부측면에서 예산 수립과 자원관리에 효율성을 담보할 수 있을 것이다.