1. 서 론
2. 수치모의
2.1 기본 이론
2.2 지형자료 구축
2.3 경계조건
2.4 FLO-2D 모형 검증
3. 결과 및 분석
3.1 토석류 전파특성
3.2 토석류 흐름특성
4. 결 론
1. 서 론
토석류는 집중호우, 지하수 등이 함수율을 급격히 증가시켜 지반이 무너져 내려 암석과 같은 큰 입자들을 포함하여 혼합체의 형태로 흘러 내려오는 현상이다(O’Brien and Julien, 1985; Kim and Seo, 1997; Iverson et al., 2001; Jeong, 2010, 2011). 지하 수위 증가로 퇴적층 상단부에 부유력이 작용하며 발생하는 부유력은 사면안정성을 붕괴시켜 토석류를 유발한다(Xi-lin et al., 2000). 따라서 퇴적층이 수용 가능한 양의 강우가 발생했을 때는 서서히 유출되어 사면이 붕괴 되지 않는다. 그러나 최근 기후변동성으로 인해 국지성 게릴라 집중호우가 증가하고 있으며 국지성 게릴라 집중호우는 산지의 토사 퇴적층의 지하수위를 증가시켜 산지 주변 건물이나 사람이 토석류로 인한 위험에 노출되고 있다.
국내는 산지는 행정구역면적 중 약 9,968,000 ha(99,680 km2)를 차지하고 있으며 행정구역 대비 최대 82%(강원도), 평균 52%를 차지하고 있어 지리적으로 산지 비율이 높다(Korea Forest Service, 2007). 도시인구집중으로 인해 한정된 도시공간에 인구, 주거시설 및 편의시설 등이 증가하여 산지 주변까지 위치하고 있다. 산지 주변에 위치한 인구나 주거시설 등은 토석류 재해의 영향권에 속한다. 이에 따라 토석류의 흐름양상을 파악하여 토석류로 인한 피해예방에 대해 지속적인 연구가 필요하다.
2011년 발생한 우면산 산사태로 인해 인명 및 재산피해가 발생한 이후 지속적으로 토석류에 대한 관심이 높아졌으며 이로 인해 관련된 연구가 활발히 진행되고 있다. Kim et al.(2019)는 사방댐 위치변화에 따른 토석류의 충격력을 검토하였으며 Lee et al.(2015)는 전파면의 경사에 따른 토석류의 거동특성 및 전파거리를 FLO-2D를 활용하여 검토했다. Kim et al.(2013)은 우면산 토석류의 전파길이를 FLO-2D를 통하여 분석하였다. Lee and Kim(2013), Kim et al.(2019)은 토질특성에 따른 토석류의 거동을 FLO-2D로 분석하였다.
Scheidl et al.(2019)은 토석류의 상·사류 흐름에 대한 거동특성을 분석하였으며 유동학적 모델과 유동학적 실험을 기반으로 한 수치해석 기법이 지속적으로 개발되었으며, 개발된 수치해석 프로그램을 통한 모의결과와 실제 토석류의 전파범위나 토석류의 유속, 수심 등을 비교 및 분석한 연구가 활발히 진행되어 왔다(Iveson et al., 2001; Iverson, 2003; Rickenmann et al., 2006; O’Brien et al., 1993).
본 연구에서는 경사지 형상과 토석류의 흐름양상을 연관한 연구를 진행하였다. 국내에서 경사지 형상에 대한 중요도를 간과하고 있다. Table 1은 기존의 경사지 재해 위험도 분석의 주요 분석 요소를 나타내고 있다. 행정안전부, 산림청 그리고 도로공사에서 실시하는 경사지 재해 위험도 평가를 살펴보면 평균경사와 같은 토석류의 특성에 대한 조사와 피해시설 및 인구와 같은 통계적인 수치자료를 종합적으로 활용하여 평가한다. 도로공사는 경사지에 대한 검토를 점수화한 재해점수와 토석류에 대한 대책을 점수화한 취약점수로 나누어지며, 재해점수에는 경사지 형상에 대한 점수는 포함되지 않으며 유역의 평균경사나 경사분포를 통해 점수를 정한다. 경사지 형상에 대한 토석류의 위험도 평가는 행정안전부와 산림청에서만 검토되고 있다. 산림청에서는 계류 상부 경사를 통해 경사지 형상에 대한 검토를 대체하는 것으로 볼 수 있으며, 이는 최대 점수 687점 중 54점으로 약 8%에 해당하며 행정안전부는 최대 141점 중 경사지 형상에 대한 점수는 4점, 3%에 불과하다. 이는 경사지 형상에 대한 검토를 기존의 경사지 위험도 분석 3가지에서 간과하고 있다.
Table 1.
Debris flow evaluation parameters of each governmental agency
| Contents | MOIS1) | KFS2) | KEC3) |
| Average Slope | ○ | ○ | ○ |
| Length of Slope | ○ | ○ | |
| Profile Shape of Slope | ○ | ○ | |
| Groundwater | ○ | ||
| Expected victim and property damage | ○ | ○ | ○ |
| Accumulation characteristic | ○ |
따라서, 본 연구에서는 토석류의 거동특성을 경사의 형상에 따라 검토하여 수치모의를 통해 경사지형상을 일반화시켜 흐름양상의 차이를 검토했다. 실제 지형의 경우 복합적으로 나타나는 흐름특성으로 인해 토석류의 형상이 토석류의 흐름양상에 미치는 영향을 확인할 수 없기 때문에 토석류의 흐름을 잘 검토하고 있다고 평가되고 있는 FLO-2D 프로그램을 사용하여 수치모의를 수행하였으며 토석류 피해 규모가 컸던 도심지 소규모 산지에 단일형태 경사면의 종단면을 각각 볼록형, 오목형, 기본형으로 나누어 전파면과 경사면에 대해 유속, 수심, 충격응력 등 토석류의 흐름양상을 분석하였다.
2. 수치모의
2.1 기본 이론
FLO-2D는 O’Brien et al.(1993)이 미국 콜로라도 주립 대학에서 유한차분법을 기반으로하여 개발한 프로그램이다. 해석범위를 크기가 일정한 격자로 나누어 범람, 홍수, 유역강우 및 유출, 해일, 토사이동 및 토석류 등을 포함하는 홍수 위험을 예측하여 관련 지도를 작성하는 2차원 해석 소프트웨어로 토석류 해석에 있어 전파범위에 대한 해석이 우수하여 국내 경사지 위험도 평가에 상용화되어 있는 프로그램이다. 단, FLO-2D는 하상침식을 고려할 수 없는 점과 격자 당 유량입력 제한이 있다는 단점이 있다. Eqs. (1), (2) & (3)은 FLO-2D에서 적용되는 지배방정식으로 에너지방정식과 운동량방정식을 기반으로 구성되어 있다.
| $$\frac{\partial h}{\partial t}+\frac{\partial(uh)}{\partial x}+\frac{\partial(vh)}{\partial y}=i$$ | (1) |
| $$S_{fx}=S_{bx}-\frac{\partial h}{\partial x}-\frac{\partial u}{g\partial t}-u\frac{\partial u}{g\partial x}-v\frac{\partial u}{g\partial y}$$ | (2) |
| $$S_{fy}=S_{by}-\frac{\partial h}{\partial y}-\frac{\partial v}{g\partial t}-u\frac{\partial v}{g\partial x}-v\frac{\partial v}{g\partial y}$$ | (3) |
여기서, Sfx, Sfy는 x방향과 y방향의 마찰경사이며 h는 토석류의 수심, u와 v는 수심을 통해 산정되는 x 방향과 y 방향의 마찰경사이다. 경사면에 발생하는 전단응력(τ)은 Eq. (4)와 같이 산정된다.
| $$\tau=\tau_c+\tau_{mc}+\tau_v+\tau_t+\tau_d=\tau_y+\eta(\frac{\partial u}{\partial y})+C(\frac{\partial u}{\partial y})^2$$ | (4) |
여기서, τy(=τc+τmc)는 항복전단응력, τc는 결합항복응력, τmc는 Mohr-Coulomb 응력 τν는 점성전단응력, τt는 난류전단응력, τd는 분산전단응력, η는 동점성 계수, C는 내부전단응력이다.
총 전단응력을 수심적분하여 경사형식(gradient form)으로 표현하면 Eq. (5)와 같다.
| $$S_f=S_y+S_{nu}+S_{td}=\frac{\tau_y}{\gamma_mh}+\frac{k\eta u}{8\gamma_mh^2}+\frac{n^2u^2}{h^{4/3}}$$ | (5) |
여기서, Sy는 항복경사, Sν는 점성경사, Std는 난류-분산경사, γm는 유사혼합물의 비중량, κ는 저항매개변수 n은 등가 조도계수 값이다.
2.2 지형자료 구축
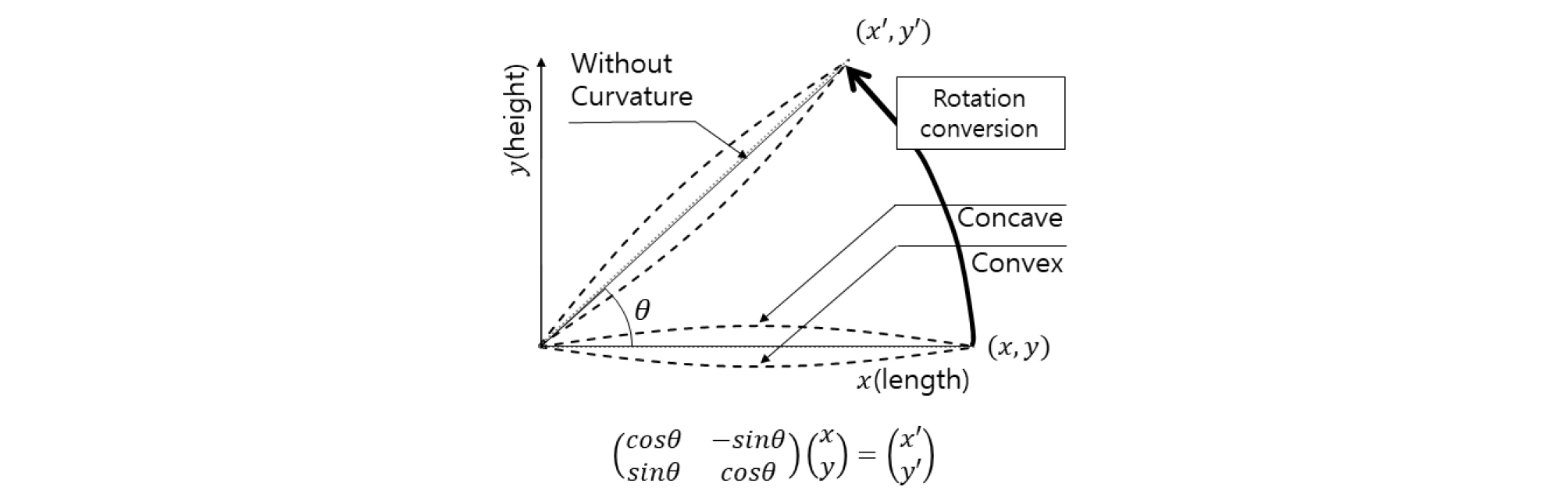
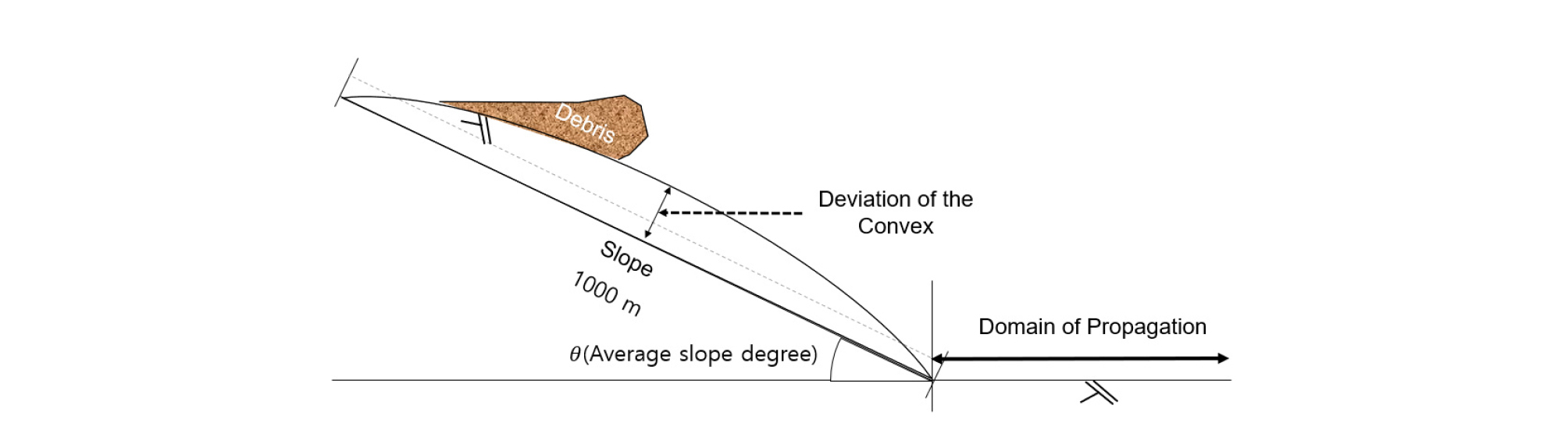
지형자료는 경사면의 형상에 따른 차이를 살펴보기 위해 경사면 형상을 기본형(Without Curvature), 볼록형(Convex), 오목형(Concave)으로 나누어 구축했다. 각 경사면은 Table 2에 정리한 바와 같이 , 함수폭은 2D m 주기는 P m 인 sine함수 형태로 구성 후 회전변환을 시켜 구축하였다. 백양산, 우면산 등토석류로 인한 피해가 발생하는 도심지 내 산지의 경사면의 계곡 길이는 1,000 m 내외로 나타나며, 계산의 편의를 위해 경사길이를 1,000 m(주기 2,000 m)를 기준으로 검토하였다. 경사면의 형상을 표현하기 위해 평균경사와 동일한 기울기를 같는 점선의 접점과 기본형 경사와의 차이를 공차(Deviation)로 정의한다. 볼록형을 양수, 오목형을 음수로 나타냈으며 기본형 경사는 직선형태의 경사를 나타낸다. 공차가 일정수준 이상이 되면 전파면보다 경사면의 고도가 낮아져 웅덩이가 만들어진다. 따라서 흐름양상에 대한 검토가 가능할 수 있는 적절한 공차를 검토하여 볼록형과 오목형은 각각 50 m의 공차를 통해 나타내며, 공차의 발생 위치는 경사의 중앙인 500 m 지점으로 하여 지형은 대칭을 이룬다. 구축된 함수를 Fig. 1와 같이 평균경사 θ만큼 회전변환을 시킨 결과, Fig. 2와 같이 경사면이 나타난다. Jakob and Hungr(2005)에 따르면 일반적으로 토석류는 경사 25°에서 35° 사이 분포하고 있으며, Jang et al.(2017)이 국내의 토석류 발생 사례의 경사별 분포를 살펴보면 경사 40° 이하인 경우가 73%를 차지했다. 이에 따라 30°를 기준으로 정하고 직관적인 결과 확인을 위해 일정 간격으로 경사각을 15°, 30°, 45°로 각각 구축하였다.
Table 2.
Initial geometric pattern function of bed slope
| Curvature of bottom slope | Initial function (Before Rotation) |
| Without Curvature | y= 0 |
| Convex | |
| Concave |
2.3 경계조건
FLO-2D 내에서 토석에 대한 물성치는 항복응력과 동점성계수로 결정된다. 2가지의 변수에 대한 식과 선행 연구로 나타난 계수는 Table 3과 같다. O’Brien and Julien(1988)이 각각 다른 지형조건을 적용한 실험으로 얻은 값이다. Lee and Kim (2013)는 항복응력과 동점성계수를 결정짓는 값의 변화 따른 FLO-2D에서의 토석류의 거동을 연구한 결과 그 값에 따라 결과가 차이가 났다. 본 연구에서는 선행연구와 Table 3를 참고하여 항복응력과 동점성계수는 화강암 지반이 대부분인 국내 지형특성을 고려하여 Gleenwood1으로 설정했다(Lee et al., 2015).
Table 3.
Yield stress and viscosity data at field (FLO-2D Reference Manual, 2009)
경사면의 중앙지점(500 m)을 기준점으로 상단부와 하단부로 나누면 기준점에 대해 대칭을 이루고 있다. 공차의 영향으로 경사의 길이가 기본형 경사보다 길어지고 각도가 점차적으로 변하게 된다. 길이는 약 125 m 증가하며, 각도는 시점과 종점에서 평균경사의 경사각과 ± 8.9°의 차이를 나타내었다. 구축된 자료를 FLO-2D를 통하여 수치모의 수행을 위해 정사각 격자로 구성하였으며, 격자간격은 수치계산의 안정성을 고려하여 5 m로 설정하였다.
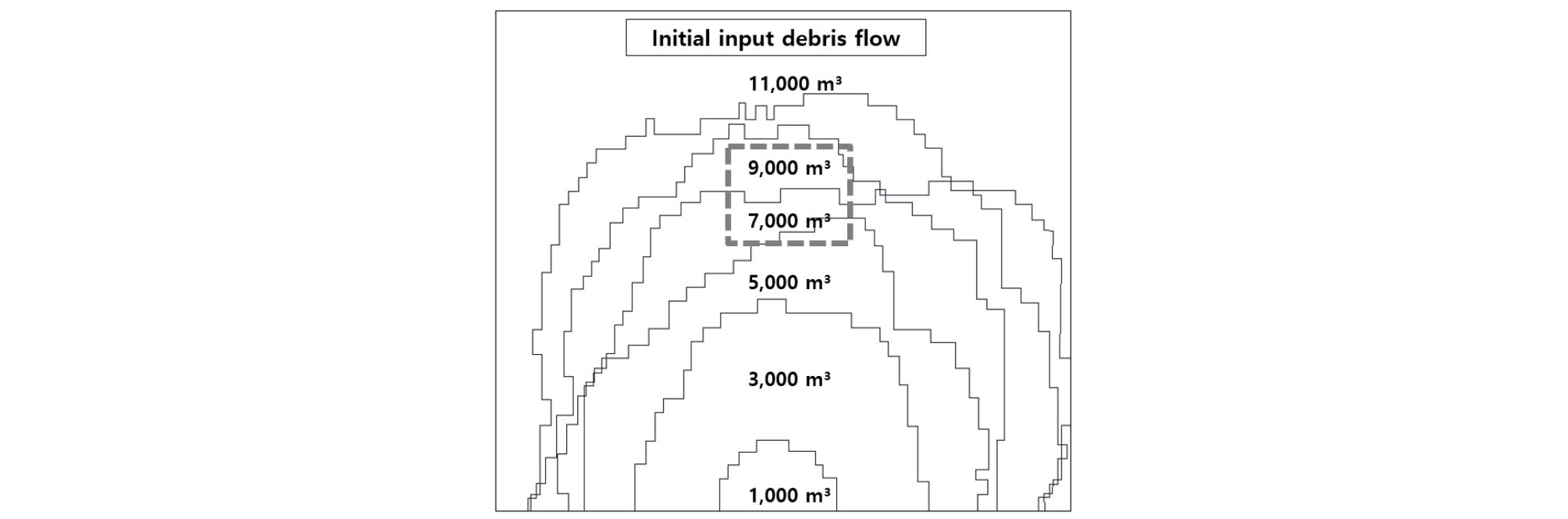
토석류 흐름양상을 명확하게 나타내는 토석류의 유입량 산정을 위해 경사 15°, 30°, 45° 중 가장 경사가 급한 45°에서 유입된 토석량에 따른 흐름양상을 살펴보았다. Fig. 3는 유입되는 토석량에 따른 전파면의 토석류의 양상을 나타낸다. 1,000 m3 부터 시작하여 2,000 m3 씩 토석량을 증가시키며 모의를 수행하였다. 300 m의 폭보다 넓게 퍼지는 11,000 m3는 제외하였으며 토석량의 경사면 길이 대비 10%인 100 m에 도달하지 않는 경우도 토석량이 적은 것으로 판단하여 적합한 조건에서 제외시켰으며 최적 유입토석량 산정 결과는 Table 3과 같다. 유입조건으로 적절한 토석류 7,000 m3와 9,000 m3 중 토석량이 많은 9,000 m3를 총 유입토석량으로 산정하였다. 그 외 추가적인 경계조건으로 조도계수는 0.04(James et al., 2014) 토석류의 비중(GS)은 2.65(O’brien et al., 2009)로 산정하였다.
주어진 유입조건 및 물성치에 대해 각 평균경사와 경사면 형상에 따라 Table 4와 같이 9가지 Case에 대해 수치모의를 수행하였다. 수치모의 시간은 도달거리의 변화가 1분간 10 m 내로 발생하는 시간을 기준으로 하여 사전 모의한 결과 45°와 30°에서는 1.0 시간, 15°에서는 1.25 시간을 수치모의 전체 모의시간으로 적합했다. 또한 시간에 따른 토석류의 흐름을 검토하기 위해 0.05 시간에 따라 수치모의를 수행하여 시계열로 결과를 나타냈다.
Table 4.
Cases of this study
| Avearage Slope | 15° | 30° | 45° |
| Without Curvature | case 1-1 | case 2-1 | case 3-1 |
| Convex | case 1-2 | case 2-2 | case 3-2 |
| Concave | case 1-3 | case 2-3 | case 3-3 |
2.4 FLO-2D 모형 검증
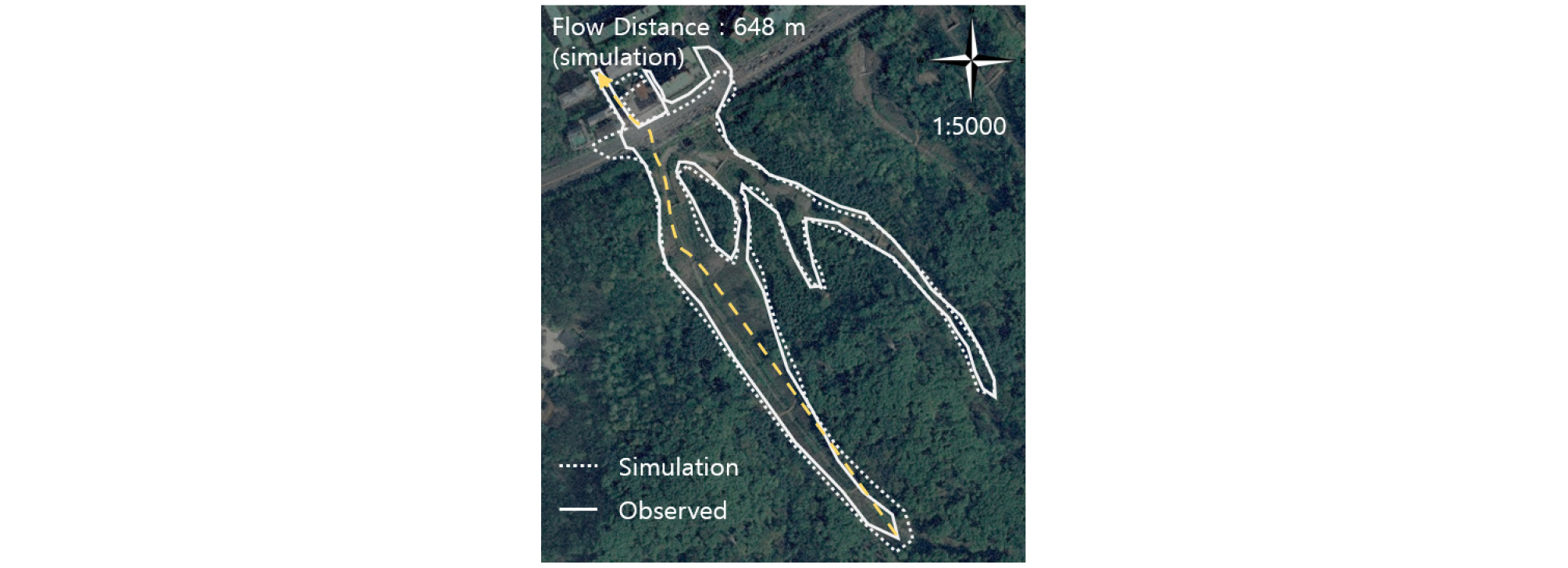
2011년 발생한 우면산 산사태 사례와 전파범위를 비교함으로써 경계조건에 대한 검증을 수행했다. 유입조건으로 토석량은 26,400 m3으로 산정하였으며(Lee et al., 2019), FLO-2D를 통해 우면산에 발생한 토석류와 관측된 토석류 피해범위를 비교해본 결과(Fig. 4), FLO-2D의 특성 토석류의 고착화를 표현하기 제한되기 일부 오차가 발생하는 것을 고려하여도 유사하게 나타났다. 토석류 도달거리는 660 m로 관측되었으며, 수치모의 결과는 648 m로 산정되어 유사도는 98.07%로 전파면적은 92% 유사한 것으로 나타났다.
3. 결과 및 분석
3.1 토석류 전파특성
3.1.1 횡단면에서의 흐름특성
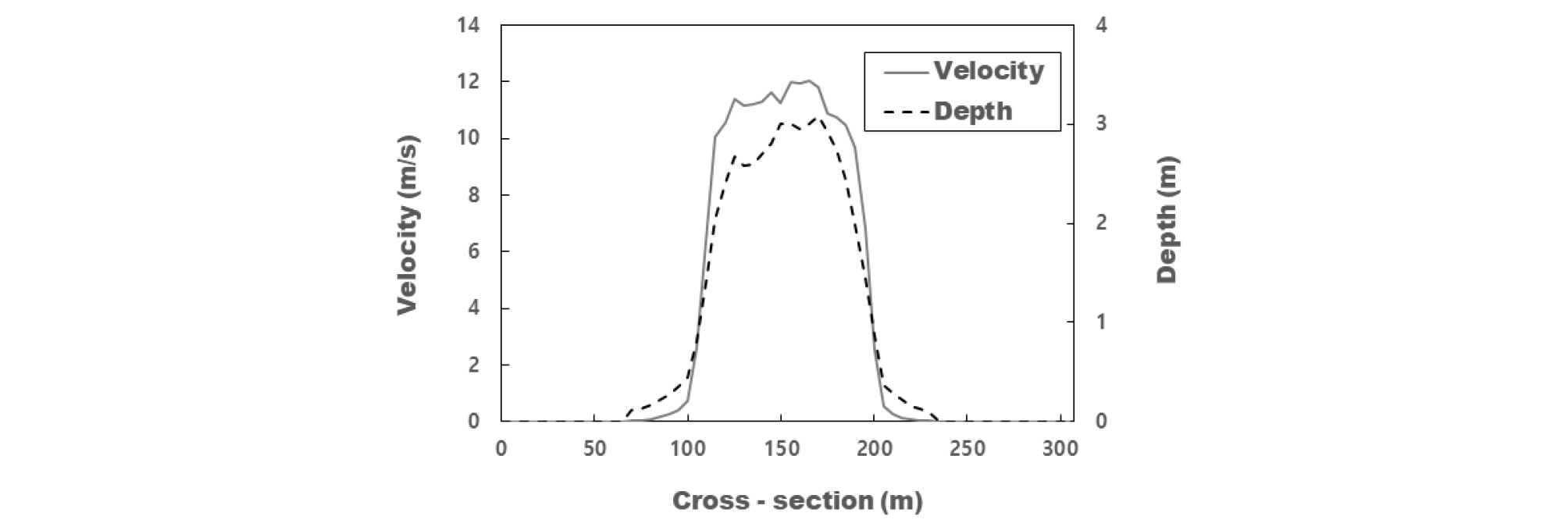
검토 경사 중 가장 급경사인 45°에서는 빠른 유속이 예상됨에 따라 공차가 없는 기본형 경사인 case 3-1을 통해 횡단면의 흐름특성을 검토하고 연구에 필요한 적정 종단면을 선정했다. Fig. 5는 Case 3-1의 전파면과 경사면의 경계, 횡단면에 발생하는 토석류의 수심과 유속의 분포를 나타낸다. 횡단면 중앙에서 유속과 수심이 극값으로 나타났다. 이에 따라 도달거리, 수심, 유속, 충격응력에 대한 수치를 횡단면의 중앙지점을 기준으로 하여 비교하였으며 발생하는 수치모의 결과를 흐름방향과 평행한 종단면으로 나타내어 토석류의 흐름양상의 변화를 관찰하였다. 토석류의 흐름양상을 검토하였다.
3.1.2 시간에 따른 토석류 도달거리
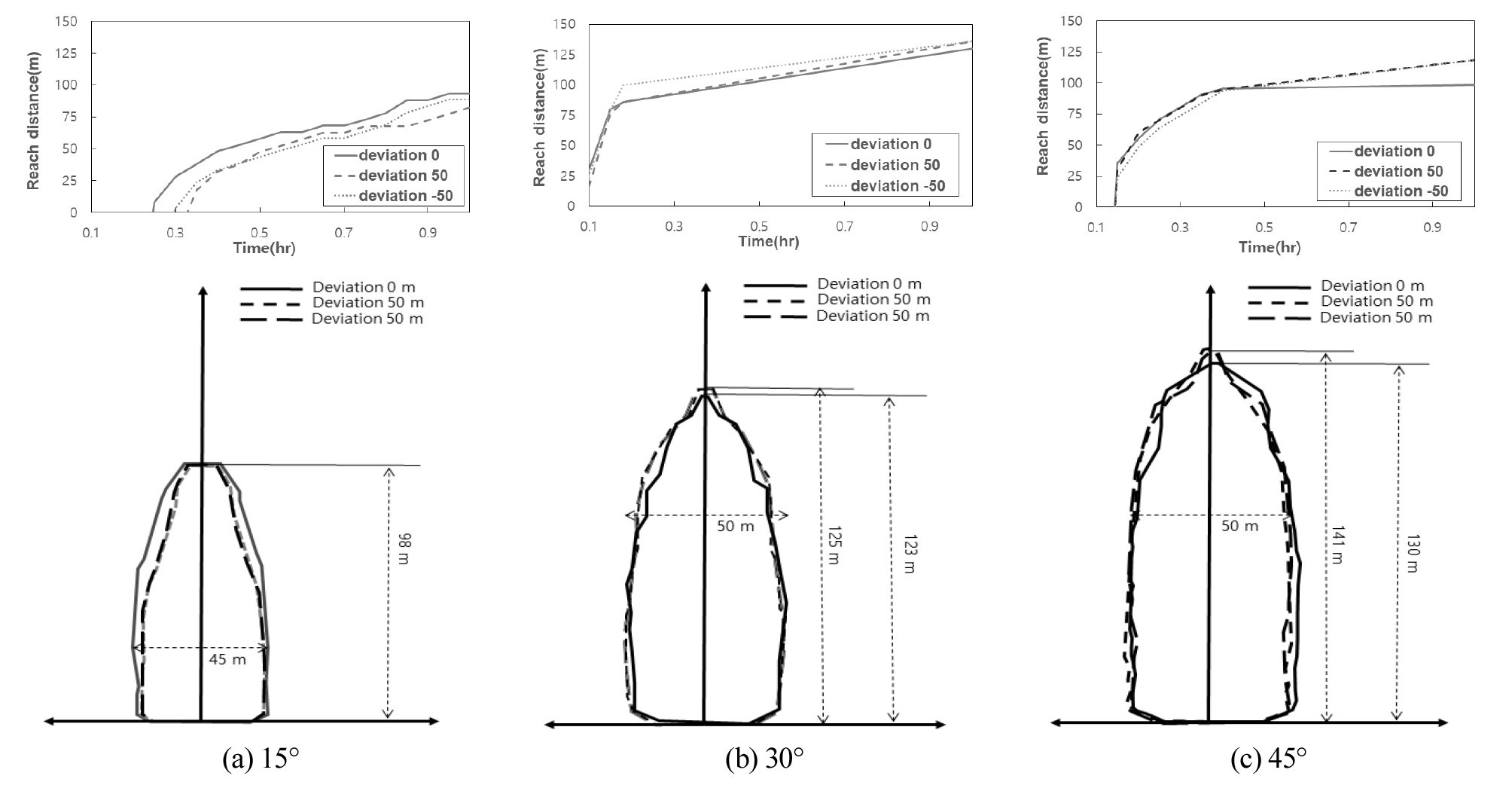
FLO-2D는 결과를 시계열로 표현하기 제한적이므로 수치모의 종료시간을 조정하여 시간에 따른 도달거리에 대한 결과를 도출하였다. 토석류는 3분이 경과된 이후 유입되며 결과에 대한 단위 시간은 0.01 시간 단위로 나타냈다. 전파면(Domain of Propagation) 에서 도달거리(Reach Distance)를 시간에 따라 나타낸 결과는 Fig. 6의 (a), (b), (c)와 같다. 최대 도달거리는 130 m로 Case 3에서 나타났다. 80 m 거리를 기준으로 하여 도달하는 시간을 검토한 결과 Case 1에서는 52분, Case 2에서는 21분, Case 3에서는 9분이 각각 소요되었다. 도달거리는 평균경사가 지배적인 흐름양상을 보였다. 가장 분명한 차이를 보인 Case 1의 경우, 전파면까지 도달하는 시간은 Case 1-1이 14분 Case 1-2는 19분, Case 1-3은 18분이 소요되었다. 이는 볼록형 경사와 오목형 경사에서 공차로 인해 경사길이가 길어지기 때문이다. Case 2와 Case 3에서는 도달시간 간 차이가 상대적으로 유사하게 나타나는데, 그 이유는 약 15 m/s 정도의 빠른 유속으로 인해 125 m를 이동하는 시간이 8초 정도 소요되며 이는 결과를 전체 시간의 1.0%미만으로 상대적으로 차이가 작다고 볼 수 있다. 또한 일정시간이 지나면 토석류의 이동이 급격히 감소하는 구간이 발생하고 토석류는 정지하게 된다. 정지상태에서의 토석류의 도달거리는 경사면 형상에 따라 차이가 발생하지 않는다. 이는 토석류의 점성과 토석의 유입량, 평균경사 등 다른 변수에 의해 정해진다.
3.1.3 토석류 전파범위
Fig. 6의 (d), (e), (f)는 72분이 경과된 이후, 토석류의 전파범위를 나타내고 있으며 최대 폭과 전파범위는 경사면 형상과 무관하게 유사하다. 가장 큰 차이를 보인 Case 3에서 볼록형과 오목형 경사에서 토석류의 도달거리가 최대 141 m, 피해범위의 최대 폭은 50 m로 기본형 경사에서 토석류의 최대 도달거리는 130 m로 볼록형과 오목형 경사의 도달거리의 92%에 해당한다. 전체 전파범위에 비해 상대적으로 적은 차이를 나타내고 있다. 위와 같은 현상은 Case 1과 Case 2에서도 동일하게 나타난다. 전파 범위는 동일한 토석류의 물성치에 대해 평균경사가 지배적이며 경사면 형상으로 인해 발생하는 토석류의 흐름양상의 차이는 전파면에 미치는 영향이 작다.
3.2 토석류 흐름특성
3.2.1 토석류 토심분포
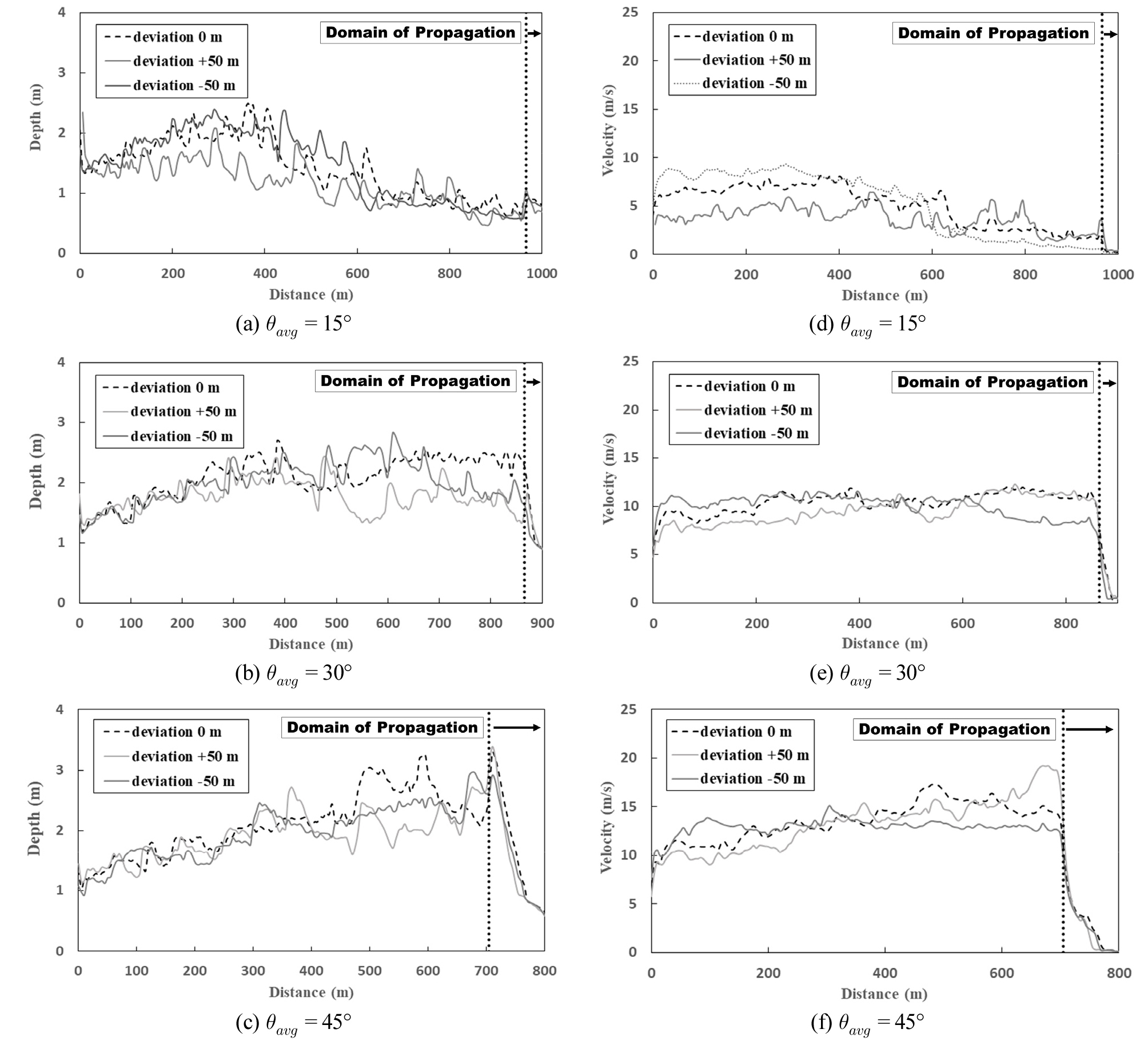
경사면에서의 흐름양상을 확인하기 위해 Fig. 7(a), (b), (c)와 같이 경사면에서 전파면까지 전구간의 토심을 검토하였다. 경사면은 평균경사와 같아지는 중앙지점을 기준으로 상단부와 하단부로 나누어 비교했다. Case 1에서 기본형 경사와 볼록형 경사는 토석류가 흘러가면서 점차 토심이 증가했다가 감소하는 추세를 보이며, 오목형 경사는 지속적으로 감소하는 추세를 보였다. Case 2에서 모든 경사는 상단부에서 증가하는 추세를 나타내고 있으며 하단부에서는 경사면에 공차가 존재하면 감소하는 추세로 바뀌게 되는데 볼록형 경사가 오목형 경사보다 감소추세로 바뀌는 임계점이 전파면과 상대적으로 멀리 있는 지점에 발생한다. 기본형 경사는 하단부에서 일정하게 유지되는 추세를 보였다. Case 3에서는 3가지 경사에서 동일하게 증가하는 추세를 확인할 수 있다. 공차가 있는 경우 토심의 증가율이 기본형 경사보다 낮게 나타난다. 토석류가 발생하면 경사면에서 정상상태가 되기 위해 토심이 증가하는데 Case 1의 볼록형 경사는 상단부 완만한 경사로 인해 마찰에 의한 감속이 더 크게 작용하므로 증가하지 않고 일정한 유속이 유지된다. Case 1의 하단부에서는 볼록형 경사가 급경사를 이루고 있지만, 0.8 m까지 낮아진 수심으로 유지되고 있는 것으로 보인다. Case 2에서는 토석류의 토심은 정상상태가 이르기 전까지, 경사형상과 무관한 흐름을 나타내지만, 중간지점(450 m) 이후 경사 형상에 따라 토심의 증감이 다르게 나타난다. 볼록형 경사에서는 토석류의 토심이 증가하고 있으나, 오목형 경사에서는 감소하고 있다. Case 3에서는 높은 경사로 인해 정상상태에 이르기 전까지 수심의 증가가 지속되어 하단부로 내려올 때까지 정상상태를 유지하지 못하여 경사형상에 따른 변화가 없다.
3.2.2 토석류 유속분포
Fig. 7(a), (b), (c)에 토석류의 유속분포를 평균경사별로 나타냈다. 토석류는 평균경사마다 경사형상에 따른 유속분포가 다르게 나타났다. 평균 유속에 따라서 Case 1에서 유속이 토석류가 유입된 이후 지속적으로 유속이 감소하고 Case 2에서는 일정구간에서 유지되고 있다. 그리고 Case 3에서 모든 경사형상에서 증가하고 있다. Case 1에서 토석류의 유입 이후 볼록형 경사는 상단부에서 완만한 경사를 이루고 있기 때문에 3~4 m/s의 유속으로 유하하고 있으며, 오목형 경사는 상단부 급경사로 인해 기본형보다 빠른 7~8 m/s의 유속이 발생하고 점차 감소하고 있다. 조도계수의 영향으로 유속은 점차 감소하고 있으며, 이는 모든 경사의 형상에서 나타나고 있다. 이때 감소하는 폭이 경사형상에 따라 다르게 나타난다. 공차로 인해 발생하는 최소 경사에서의 흐름이 마찰에 의한 감속보다 경사에 의한 가속이 더 크기 때문이다. Case 1~3까지의 결과를 토대로 경사에 따른 흐름과 마찰에 따른 흐름에 의해서 주로 토석류의 유속이 결정되고 있으며, 볼록형 경사, 오목형 경사는 기본형 경사보다 경사거리가 125 m만큼 증가하여 마찰에 감속이 되는 구간이 길어짐에 따라 발생하는 유속에 차이가 발생한다. Fig. 7(d), (e), (f)을 살펴보면 볼록형과 오목형은 400 m에서 700 m 구간에서 점대칭하는 형상이 보여진다. 평균경사가 작을수록 점대칭이 경사면 하단부에서 일어나는 것을 확인할 수 있다. 경사에 의한 유속의 영향을 살펴보기 위해 기본형 경사에 보정계수 α =1000 /1125 [m/m]를 도입하여 전파면과 경사면의 접점에서의 유속을 Table 5에 나타내었다.
Table 5.
Initial velocity of debris flow in the phase of propagation
| Average slope | Without curvature (αV) | Convex (V) | Concave (V) |
| 15° | 2.5 m/s | 4.0 m/s | 1.2 m/s |
| 30° | 6.2 m/s | 8.0 m/s | 5.0 m/s |
| 45° | 11.5 m/s | 14.0 m/s | 10.0 m/s |
전파면에 도달 했을 때의 유속에는 일정한 비율로 나타남을 확인 할 수 있다. Eq. (6)을 통해 공차와 유속 간 관계를 살펴보면 Case 1에서 경사형상에 따른 유속비는 52%에서 60%로 나타났으며, Case 2에서 유속비는 20% ~ 30%, Case 3에서 13% ~ 20%가 나타난다.
| $$\begin{array}{l}\frac{\triangle v}{v_0}\times100\%\;=E_R\;\\\triangle v=\;abs(v_{convex}-v_{std})\end{array}$$ | (6) |
여기서, v0은 기본형 경사의 유속, ER은 경사형상에 따른 유속비이다.
| $$\triangle\theta=tan^{-1}(R\times2\pi f\;cos(2\pi fx))$$ | (7) |
여기서 R은 공차, f는 주기, θ0는 평균경사이며 θ는 지면과 이루는 사잇각이다.
Eq. (7)을 통해 공차에 따른 경사각의 변화(△θ =θ-θ0)를 계산하면 최대 8.9°가 발생한다. 최대 각도변화인 8.9°는 15° 평균경사의 59.3%에 해당하는 수치이다. 반면에, 45° 평균경사에서는 19.7%에 해당한다. 각도의 변화는 상수형태로 나타나므로 경사가 낮을수록 상대적으로 경사의 변화가 커지고 이로인해 유속의 변화가 커지게 된다. 유속분포의 Eq. (7)에서 산정한 공차에 따른 θ의 변화와 비교하면 유사한 추세로 변화한다. 단, 마찰응력, 점성응력 등의 요소에 의한 차이로 인해 오차가 발생한다.
3.2.3 토석류 충격응력 분포
토석류의 이동에 따라 경사면과 전파면에 발생하는 충격응력을 분석하였다. FLO-2D에서 수치모의를 통해 분석한 토석류에 의한 충격응력은 Eqs. (8) & (9)을 바탕으로 산정할 수 있으며 충격이 발생하는 각도, 유체의 밀도 등과 같은 유체의 여러 요소의 영향을 받는다(FLO-2D, 2004).
| $$P_i=k\rho_fV^2$$ | (8) |
| $$k=1.261e^{C_w}$$ | (9) |
여기서 Pi는 충격응력, ρ는 밀도, k는 상수계수, V는 유속, Cw는 중량농도이다.
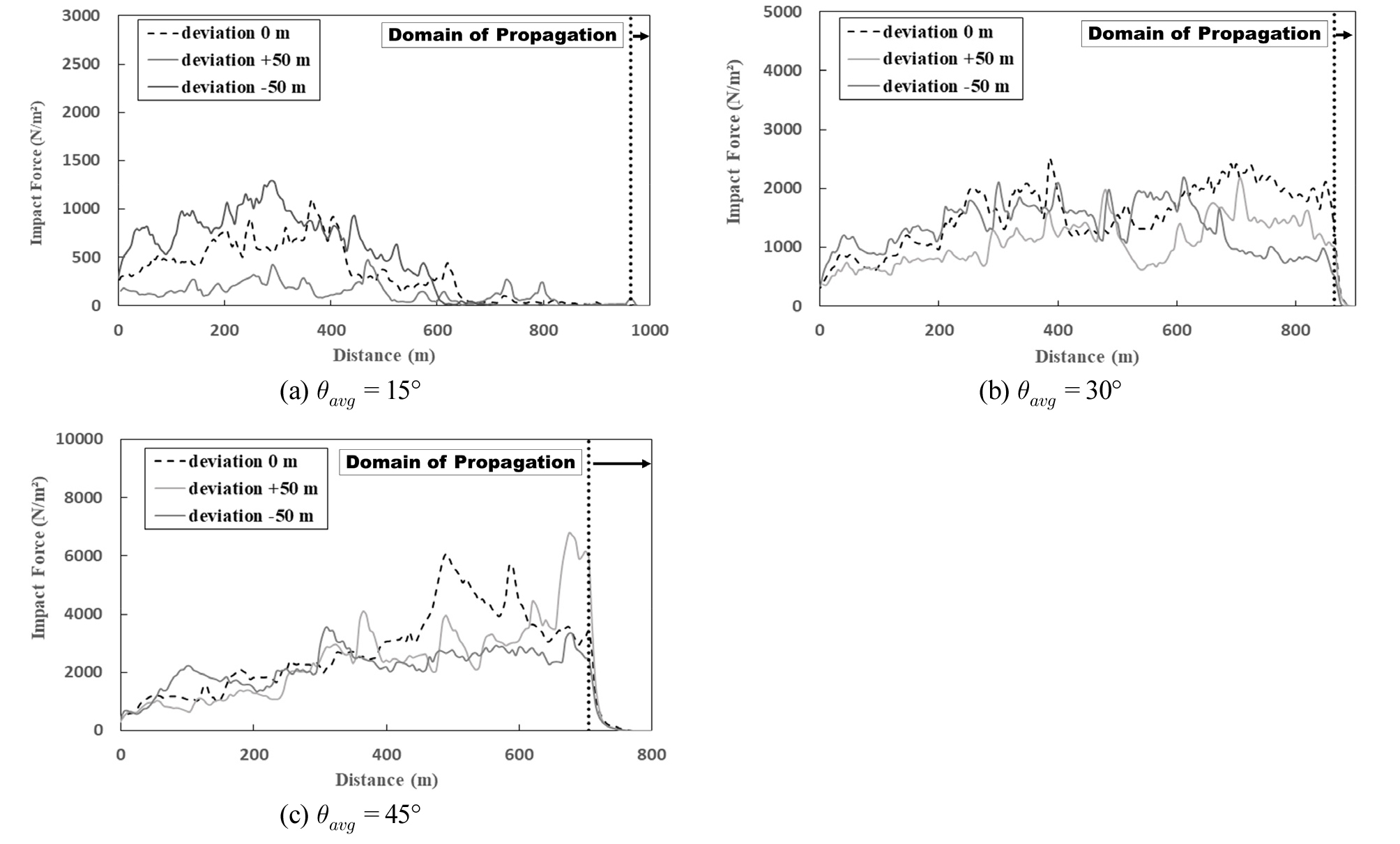
Fig. 8(a), (b), (c)는 평균경사별 충격응력을 나타내고 있으며 각 평균경사에서 오목형 경사가 전파면에 도달했을 때, 충격응력이 가장 작게 산출되었다. 충격응력은 유속의 제곱과 비례관계를 나타내고 있어 유속의 감소비율의 제곱만큼 감소하고 있으며, 공차에 따른 유속의 차이보다 충격응력이 차이가 더 분명하게 나타난다.
Case 1에서는 오목형 경사에서 충격응력이 가장 크게 발생하였으며, 해당 지점에 대해서는 유속이 10 m/s로 발생하는 지점 중에 하단부에 위치한 지점이다. 또한 볼록형 경사는 초기 토석류가 발생한 이후부터 전파면에 도달할 때까지 오목형 경사에서 발생한 최대 1500 N/m2의 20% 수준의 충격응력이 발생하였으며, 경사면 아래로 내려갈수록 유속이 점차 감소하였다. 볼록형 경사가 급경사로 변하는 지점에서 일시적으로 볼록형 경사에서 발생한 토석류의 충격응력이 증가하는 추세를 보였으나 최댓값은 500 m 지점에서 발생한 충격응력이 450 N/m2으로 가장 큰 값이다. 이는 토석류가 하단부로 내려갈수록 마찰에 의한 에너지 손실이 크게 발생하게 되는데 경사에 의한 유속의 증가보다 마찰에 의한 감속이 크게 작용하므로 발생한다. Case 2에서 발생한 토석류는 모든 경사면 형상에서 지속적으로 증가하는 추세를 나타내고 있었으며 기본형 경사가 전파면에 도달 했을 때 충격응력이 가장 크게 나타났다. Case 3에서는 볼록형 경사가 하단부에 급경사로 나타남에 따라 충격응력이 급격히 상승하는 추세를 나타나는데 하단부가 급경사기 때문에, 토석류의 경사로 인한 흐름이 마찰로 인한 흐름보다 지배적이므로 나타나는 현상으로 보인다. 토석류로 인해 발생하는 충격응력에 대한 양상을 살펴본 결과 유속이 일정량 이상이 되면 마찰보다 경사가 유속을 결정하는데 지배적이며 일정량 미만의 유속에서는 마찰이 지배적이므로 충격응력이 모든 경사면 형상에서 감소하게 된다.
4. 결 론
산지는 다양한 경사가 복합적으로 구성되어 있으며, 고도가 낮은 도심지의 경사지 형상은 전체 경사면의 형상에 따라 오목형, 볼록형, 혼합형으로 대별된다. 토석류가 발생할 수 있는 경사지 위험도 평가는 평균경사만을 이용하여 평가한다. 하지만 본 연구를 통해 경사면의 형상이 토석류의 흐름양상에 변화를 주는 것을 확인했으며, 오목형 경사와 볼록형 경사에 따라 구분하여 대책을 마련하는 것이 보다 안전하며 한편으로는 경제적인 시공이 된다. 본 연구에서는 대표 경사면 형상으로 볼록형과 오목형 경사를 선정하고 함수를 바탕으로 바닥 지형을 나타낸 후, 토석류의 흐름양상을 비교하였다. 경사면에 발생하는 공차는 경사의 길이와 각도를 변화시켜 토석류 흐름양상에 변화를 주며, 경사지 형상에 따라 평균 바닥 경사가 15°인 지형에서는 토석류의 (10)유속과 토석류로 발생하는 충격응력이 경사면에 따라 흐름양상의 변화가 가장 크게 나타났다. 이를 식과 같이 충격량의 비로 무차원화 하여 나타내었다.
| $$E_d=\left(\frac{V(s)}{V_0(s)}\right)^2\times100\%$$ | (10) |
여기서, V0(s)는 기본형 경사에서 속도, V(s)는 볼록형 또는 오목형 경사에서의 속도를 나타낸다.
| $$Impact\;acceleration\;with\;deviation=\frac{Ratio\;of\;impact}{Spatial\;change\;of\;bed\;slope}$$ | (11) |
평균경사와 공차로 발생하는 경사의 비율이 유속과 동일한 비율로 증감되는 경향을 나타내었으며, Fig. 9은 유속을 식 (10)과 같이 경사길이 비에 따른 속도의 비의 제곱으로 공차가 토석류 흐름양상에 미치는 영향을 나타내었다. Fig. 9(a)에서 나타낸 바와 같이 볼록형은 우상향 곡선으로 오목형은 우하향 곡선으로 대칭되어 나타난다. 공차의 영향을 나타내는 Ed의 값이 100%에 가까울수록 공차로 인한 영향이 적으며 대칭되는 중간 구간에서 영향이 가장 적고 상대적으로 경사가 낮을수록 상단부에 미치는 영향이 커진다. 즉, 상단부에 사방시설을 설치한다면 오목형 경사의 경우 하단부 방향으로 내려올수록 사방효과가 최대 1.6배 증대되고, 반대로 볼록형 경사는 상단부로 올라갈수록 최대 3.4배 효율이 증대된다. 식(11)과 같이 공차로 생겨나는 기울기에 따른 충격량의 변화율로 나타낸다. Fig. 9(b)에서 경사변화로 인한 토석류의 흐름양상을 확인 할 수 있으며 평균경사가 클수록 경사변화에 따른 충격량의 변화조기에 발생하며 평균경사가 낮을수록 변화폭이 크게 나타나는 것을 확인할 수 있다. 이를 바탕으로 충격량이 증가지점과 감소지점을 파악함으로써 건축물의 위치를 산정할 때 용이할 것으로 판단된다. 본 연구를 통하여 사방시설을 설치 시에는 평균경사와 경사형상을 동시에 고려하여 최대 충격량이 발생하는 곳에 사방시설을 설치함으로써 토석류의 에너지를 크게 손실시키거나, 방어 시설물을 건설할 때 최대 충격량이 발생하는 위치를 파악하여 건설한다면, 향후 발생 가능한 토석류 피해로부터 인명손실이나 경제적 손실을 최소화 할 수 있을 것으로 기대한다.