1. 서 론
지문인식, 홍채인식, 내비게이션 등의 기술은 출범 당시 혁신적이었지만 현재는 실생활에 다양한 분야에서 널리 이용되고 있다. 이 편리한 기술이 가능하게 한 배경에는 형상의 유사한 정도를 측정하는 방법 및 기술이 자리잡고 있다. 현재 형상비교 등에 대한 기술은 우리주변에 다양한 분야에서 사용되고 있으며, 공간을 표현하는 공간정보, 토지 면적 정형화에도 큰 활용성을 가진다. 최근 다양한 공간정보를 쉽게 접할 수 있고, 같은 공간에 대해서도 다수의 공간정보를 활용할 수 있다. 이러한 공간정보는 구축시기, 생산주체, 생산방법 등이 다양하기 때문에 이용자의 수요에 따라 적합한 정보를 활용해야한다. 그러나 최근에는 이용자의 수요에 관계없이 공간정보의 정확도를 확보하고 다원화된 공간자료를 통합하기 위하여 공간정보의 연동이 강조되고 있다. 재난분야에서도 재난대응을 위한 침수예상도를 제작하는 등의 공간정보에 대한 활용성이 증가하고 있으나, 재난 위험지도의 관리주체 및 생산년도, 제작프로그램에 따라 관련 공간정보는 차이가 발생한다. 그러므로 , 정보의 정확도가 피해와 직결되는 재난분야에서 공간자료의 통합과 연동은 더욱 중요하다.
공간자료의 연동 혹은 공간자료의 정확도를 검증하기 위한 방법은 사용된 기준에 따라 기하학적, 위상학적, 의미론적 방법론으로 구분할 수 있다(Tong et al., 2009). 기하학적 방법론은 거리, 방위, 위치, 형상 등의 특성으로 형상의 유사정도를 계산하는 방법으로 가장 일반적으로 사용된다. 하지만 대부분 점이나 선형 객체를 이용한 연구가 대부분이며, 면 객체를 직접 이용한 연구는 미비하다. 침수예상도의 경우 위험도 등급 별 침수 면적이 중요하기 때문에 면 객체의 비교가 필요하다. 면 객체와 관련된 선행연구로는 Ali(2001), Samal et al.(2004), Wenjing et al.(2008), Fu and Wu(2008), Huang et al.(2010)이 있다. 이들은 면 객체를 직접 이용하여 기하학적 특성을 위치, 면적, 형상으로 구분하여 방법론을 제안하였으며, Ali(2001)를 제외한 연구자들은 각 기준의 유사도에 가중치를 산정하여 통합 형상유사도를 분석하였다. 국내에서는 이들의 한계점인 임계값 설정을 보완한 CRITIC(CRiteria Importance Through Intercriteria Correlation)방법으로 동일한 지역의 공간자료간의 유사(similarity)와 차이(difference)를 분석한 바 있다(Kim et al., 2011). 김지영(Kim et al., 2011)은 위치, 형상, 면적기준을 비교하는 CRITIC 기법으로 건물객체의 형상유사도를 분석하였다. 그러나, 침수면적은 건물객체와 달리 복잡한 형상을 나타내고 있으며, CRITIC 기법의 형상기준을 그대로 적용하기에는 한계가 있다. 객체 형상과 관련하여 형상의 유사도를 계산하기 위한 방법으로는 저니키모멘트(Zernike Moments), 정규중심모멘트, RCCI(Reated Circumscribing Circle Index), Turning Function 등이 있다(Huh et al., 2012; Son et al., 2010; Kim et al., 2006; Arkin et al., 1991). 저니키모멘트는 객체 쌍의 기수성에 영향을 받지 않고, M:N 면 객체 쌍의 형상유사도를 측정할 수 있는 방법이다. 정규중심모멘트를 이용한 형상유사도 측정(Son et al., 2010) 또한 M:N 또는 1:N 매칭에 적용하기 적합한 방법이다. 이는 객체의 공간적인 분포특성을 나타낸다. 본 연구에 사용되는 면 객체는 재난발생 조건에 따라 1:1 객체 쌍이 존재한다. 또한 재난 위험도는 다수 객체의 분포특성보다는 각 개체 쌍의 유사도가 중요하다. 각 객체 쌍의 형상을 비교할 수 있는 인자로는 RCCI와 TF가 있다. RCCI는 객체의 최소 경계원에 대한 해당 객체의 면적비율을 의미하며, 해당 객체의 형상의 선형성을 측정하는데 사용된다(Kim et al., 2006). 그러나, 형상지수나 RCCI의 경우 침수면적의 복잡한 형상을 구별하기에 한계점이 있다. Turning Function(Arkin et al., 1991)의 경우 객체의 누적길이와 각도를 측정하여 객체의 형상을 측정하는 방법으로 객체의 스케일에 영향을 받지 않지만, 형상의 길이와 각도를 통해 방향성을 가지며 가늘고 긴 형상에 적용할 수 있다. 따라서, 본 연구에서는 RCCI와 Turning Function을 추가적으로 적용하여 CRITIC의 형상기준을 수정하였다.
한편, 이상기후로 인해 발생하는 재난에 대응하기 위하여 다양한 재난 대책을 수립해왔지만, 최근에는 국내 여건상 구조적 대책보다는 침수예상도 제작과 같은 비구조적 대책이 주로 수립되었다. 침수예상도 제작을 위해서는 수치모의를 통해 해당 지역의 재난 위험도를 예측해야 하나, 기존의 모형은 계산시간이 길어 골든타임 이내에 대책을 수립하기가 어려운 실정이다. 따라서 과학적 보간기법을 기반으로 한 단기간 위험도 예측 모형인 SIND을 개발하였다(Kim et al., 2018). SIND 모형을 통하여 생성된 위험지역 결과는 위치, 면적, 형상 등의 정확도가 중요하기 때문에 결과 검증이 필수적이다. 따라서 본 연구에서는 국립해양조사원에서 구축한 폭풍해일에 대한 침수예상도(KHOA, 2014)와 SIND 모형 결과의 면 객체자료를 대상으로 수정된 CRITIC 기법을 적용하였다. 재난분야에서 사용되는 위험도 지도의 면 객체 형상비교를 위한 최적의 형상기준을 도출하였으며, 재난분야에서 수정된 형상유사도 방법론의 적용성을 검토하였다.
2. 본 론
2.1 형상유사도
2.1.1 CRITIC 기법
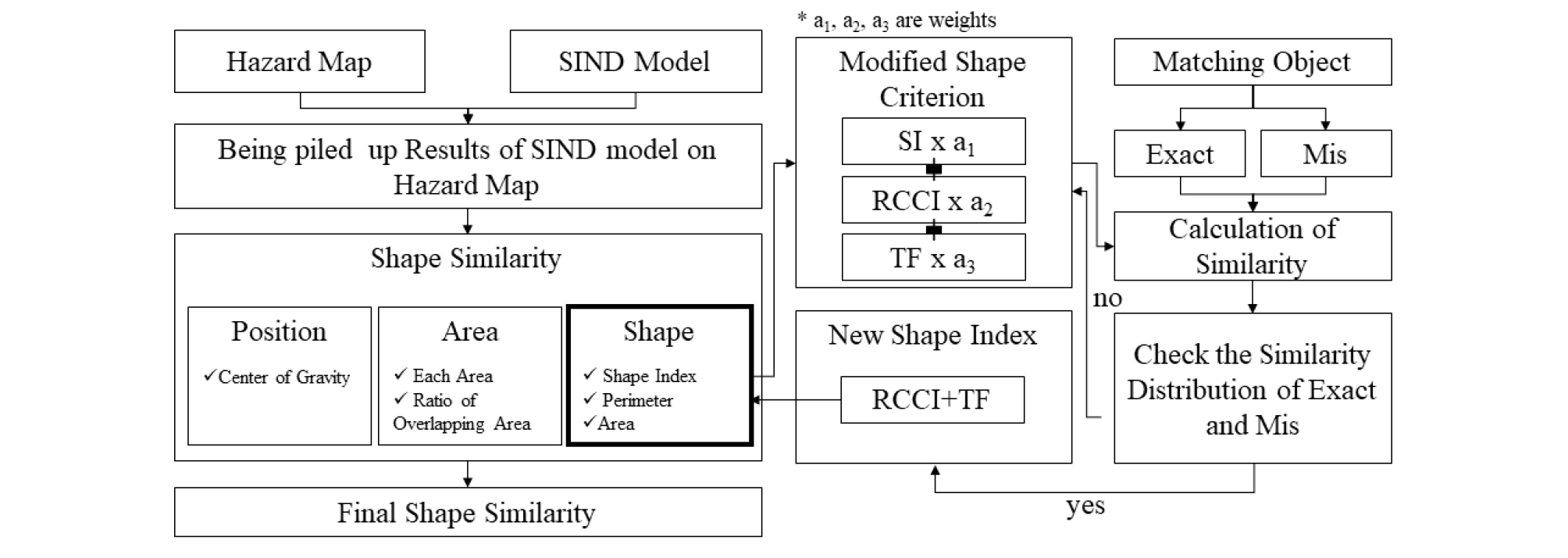
침수예상도와 SIND Model 결과의 객체들을 중첩시켜 총 175개의 매칭 쌍을 도출한 후 CRITIC 기법을 적용하였다. CRITIC 기법은 위치기준, 면적기준, 형상기준을 통해 형상유사도를 평가하는 기법이다(Fig. 1). 각 기준간의 상관관계를 이용하여 가중치를 설정하였다. 본 연구에서는 CRITIC방법의 위치기준과 면적기준을 기존의 방법과 동일하게 적용하였으며 침수예상도의 형상 특성을 반영할 수 있게 형상기준을 수정하여 적용하였다. 침수예상도는 국립해양조사원(2014)에서 제작한 것으로, 폭풍해일로 인한 연안침수 위험지역을 도면으로 표현한 것이다. 각 50년, 100년, 150년, 200년 빈도별 및 폭풍해일 시나리오를 모두 합친 최대범람역 해안침수예상도를 나타내었다.
1) 위치기준(RP, Position Criterion)
위치기준은 하나의 매칭 쌍에 속한 두 객체의 무게중심간의 거리로 평가한다. 침수예상도 객체의 무게중심은 PA, SIND 모형의 결과로 도출한 객체의 무게중심은 PB이며, 각 객체 쌍마다 무게중심 거리의 최대값을 이용하여 정규화시켜 위치기준을 도출하였다. 위치기준이 1에 가까울수록 SIND 모형의 객체는 침수예상도와 유사하다고 볼 수 있다(Eq. (1)).
| $$RP=1-(P_A,P_B)/max(P_{Aall},P_{Ball})$$ | (1) |
여기서, (PA,PA)는 무게중심간의 거리로 이다. XA와 YA는 각 매칭쌍의 무게중심 좌표이다.
2) 면적기준(RA, Area Criterion)
면적기준은 두 객체의 중복면적비를 이용하여 평가하였다. 중복면적비는 두 면 객체의 전체면적에서 중복면적을 뺀 대칭차(symmetric difference)와 면 객체 쌍의 면적 합과의 비로 정의하였으며 위치기준과 마찬가지로 각 객체의 중복면적비의 최대값을 이용하여 정규화시켰다(Eq. (2)). 면적기준이 1에 가까울수록 SIND 모형 결과와 침수예상도는 유사하다고 볼 수 있다(Eq. (3)).
| $$OA(A_A,A_B)=\vert(A_{(A\cup B)}-A_{(A\cap B)})/(A_A+A_B)\vert$$ | (2) |
| $$RA=1-OA(A_A,A_B)/max(OA(A_{Aall,}A_{Ball}))$$ | (3) |
여기서, OA(A, B)는 중복면적비이며, A는 각 매칭쌍의 면적이다.
3) 형상기준(RS, Shape Criterion)
CRITIC 기법에서 정의한 형상기준은 형상지수의 차를 말한다(Eq.(4)). 면 객체의 면적과 둘레는 양의 상관관계를 보이는 특성을 이용하여 크기와 형상지수 사이에도 양의 상관관계를 가진다는 것을 이용하였다(Burghardt and Steimiger, 2005). 각 객체 쌍의 형상지수의 차를 계산하였고, 차이의 최대값을 이용하여 정규화 하였으며, 형상 기준이 클수록 두 객체는 유사하다고 볼 수 있다(Eq. (5)).
| $$SI_{dif.}(A,B)=\left|\frac{P_A}{2\sqrt{\pi A_A}}-\frac{P_B}{2\sqrt{\pi A_B}}\right|$$ | (4) |
| $$RS=1-SI_{dif.}(A,B)/max(SI_{dif.}(A_{all,`}B_{all}))$$ | (5) |
여기서, SIdif는 두 객체의 형상지수 차이를 말하며, P는 각 객체의 둘레, A는 각 객체의 면적을 의미한다.
4) 형상유사도(R, Shape Similarity)
각 위치기준, 면적기준, 형상기준을 이용하여 최종적으로 형상유사도의 값을 도출한다. 각 기준을 적용한 형상유사도를 도출하기 위해서는 가중치를 결정해야 하는데, CRITIC 기법에서는 각 매칭기준의 정보량과 표준편차, 매칭 기준간의 상관관계를 이용한다(Eq. (6)). 즉, 각 기준들간의 상관관계를 고려하여 가중치를 결정한다. 이 가중치를 이용하여 Eq. (7)과 같이 형상유사도를 계산하며, 형상유사도의 값이 1에 가까울수록 두 객체는 서로 유사하다고 볼 수 있다.
| $$w_j=\frac{C_j}{{\displaystyle\sum_{k=1}^m}C_k},\;C_j=\sigma_j\times\sum_{k=1}^m\left(1-r_{jk}\right)$$ | (6) |
| $$R(A,B)=w_1\times RP(A,B)+w_2\times RA(A,B)+w_3\times RS(A,B)$$ | (7) |
여기서, Cj는 각 매칭기준의 정보량, σj는 각 매칭기준의 표준편차, rjk는 매칭기준간의 상관관계를 의미한다. wi는 각 기준의 가중치이다.
2.1.2 형상기준
침수예상도에 도시되어 있는 등급별 위험도 면적은 주로 가늘고 긴 객체의 형태가 대부분이며, 지형의 특성과도 연관이 있어 면을 이루고 있는 선 객체가 매우 복잡하게 형성되어 있다. 따라서, 기존의 CRITIC기법 형상기준의 주요인자인 면적과 둘레만으로는 위험지역의 유사도를 측정하기가 어렵다. 따라서 본 연구에서는 기존의 형상기준에 위험지역 특성을 고려할 수 있는 RCCI와 Turning Fuction을 적용하였다.
1) RCCI(Related Circumscribing Circle Index)
RCCI는 객체의 최소 경계원(Circumscribing Circle)에 대한 해당 객체의 면적비율을 의미한다. 이는 객체의 선형성을 측정하는데 사용되며, 폭이 좁고 길이가 긴 객체는 높은 값을 가지고, 나선형으로 꼬이면서 폭이 좁은 객체는 낮은 값을 갖는다(Kim et al., 2006). 각 객체의 RCCI의 차를 유사도 적용에 이용하였으며, 차의 최대값을 이용하여 정규화하였다(Eq. (9)).
| $$RCCI(A,B)=\left|\frac{A_A}{CA_A}-\frac{A_B}{CA_B}\right|$$ | (8) |
| $$RS_{RCCI}(A,B)=1-\left|\frac{RCCI(A,B)}{\max(RCCI(A_{all,}B_{all}))}\right|$$ | (9) |
여기서, RCCI(A, B)는 RCCI 값의 차이, A는 각 객체의 면적, CA는 객체가 가지는 최소 경계원의 면적을 의미한다. RSRCCI는 RCCI를 적용한 형상기준이다.
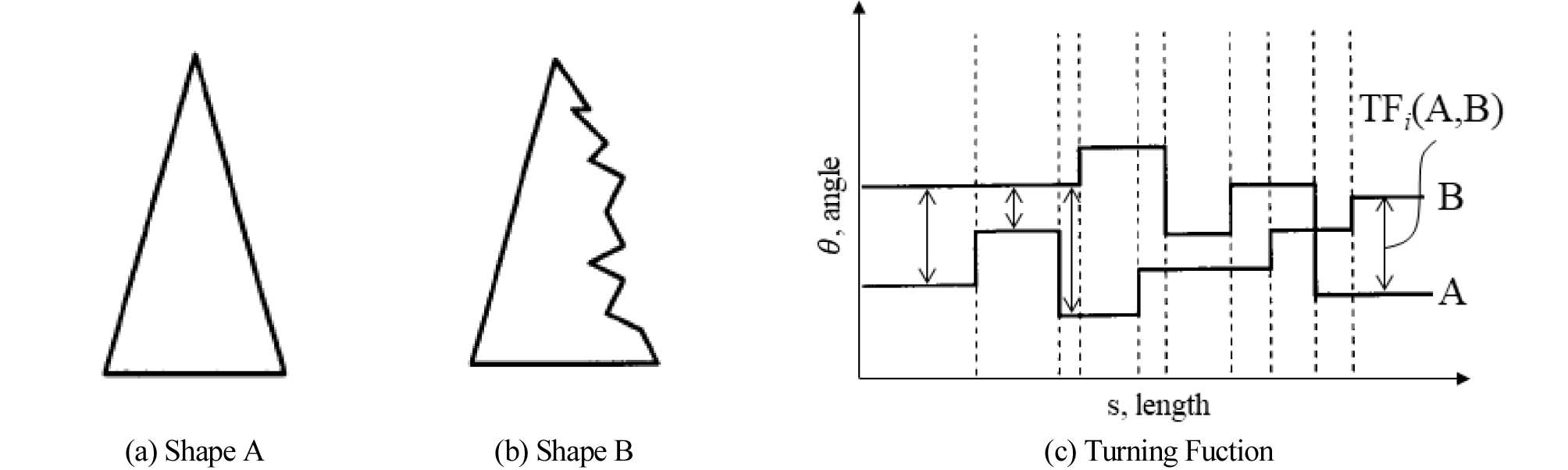
2) Turning Function
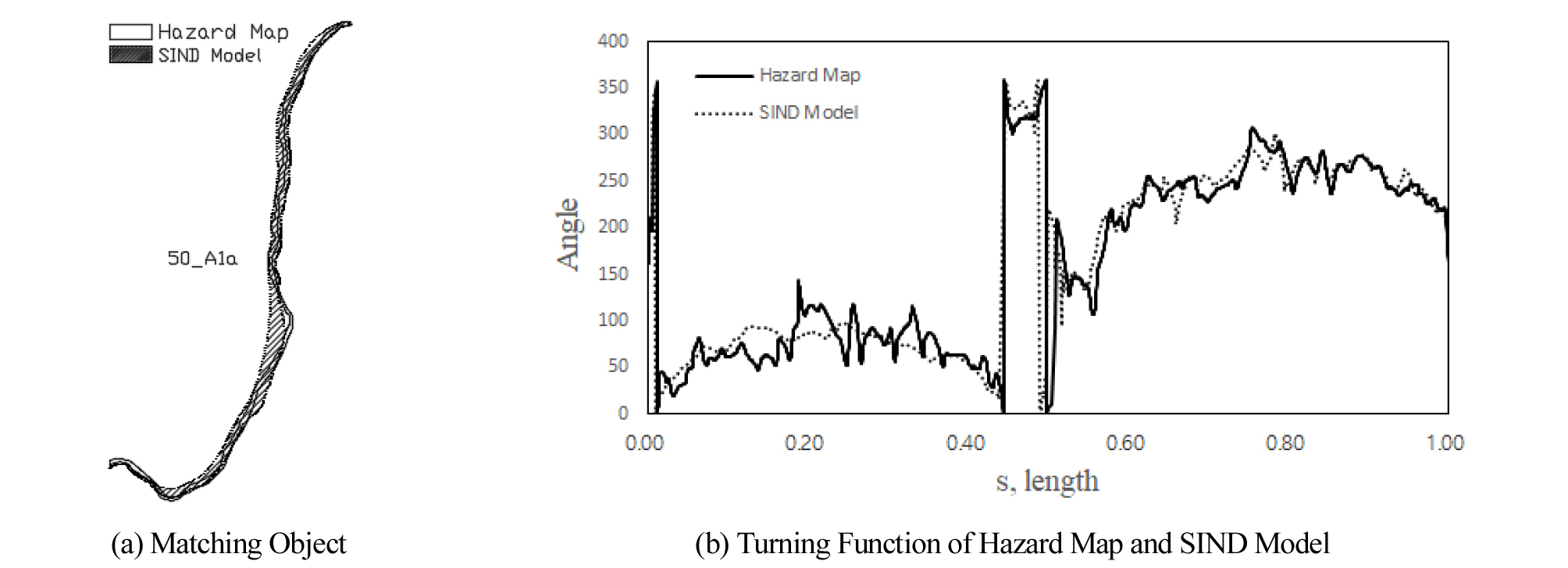
RCCI는 객체의 선형성을 나타낼 수 있지만, 가늘고 긴 객체의 방향성을 고려하지 못하는 한계점이 있다. 예를 들어, 두 객체가 똑같은 형상이지만 한 객체가 90° 회전되어있다면 두 RCCI는 값은 동일하다. 이 같은 한계를 극복하기 위해 방향성을 고려할 수 있는 Turning Fuction을 적용하였다. Turning Function은 객체위의 임의의 점에서 시작하여 반시계방향으로 객체를 선회하며 누적길이와 각 모서리의 반시계방향 각도를 측정하여 형상을 표현한다(Eq. (10)). 객체의 총 모서리 길이를 1로 정규화하여 객체의 크기와 무관하도록 하였으며, 각 객체의 형상을 표현한 선회함수간의 차이를 이용하여 두 객체의 유사도를 측정하였다. 앞서 언급한 형상기준들과 유사하게 선회함수간 차의 최대값을 이용하여 정규화하였다(Eq. (11)).
| $$TF(A,B)=\int_0^s\left|f_A\left(s\right)-f_B\left(s\right)\right|$$ | (10) |
| $$RS_{TF}(A,B)=1-\left|\frac{TF(A,B)}{\max\left(TF(A_{all},B_{all})\right)}\right|$$ | (11) |
여기서, f(s)는 각 객체의 누적길이에 대한 각도에 대한 함수식이며(Fig. 2(c)), TF(A, B)는 각 객체가 가지는 함수의 차이다. RSTF는 TF를 적용한 형상기준이다.
3) 수정 CRITIC 기법
수정된 CRITIC 기법에서는 SI, RCCI, TF를 가중치를 이용해 최적의 형상기준 값을 도출한다(Eq. (12)). 매칭 쌍의 정(exact)과 오(mis)를 명확하게 판별할 수 있도록 가중치를 도출하는 과정을 거쳐야 하며 통합 형상유사도를 도출하는 방법은 기존과 동일하다(Eq. (13)).
| $$RS_{modified}=a_1\times RS_{SI}+a_2\times RS_{RCCI}+a_3\times RS_{TF}$$ | (12) |
| $$Modified\;R(A,B)=w_1\times RP+w_2\times RA+w_3\times RS_{modified}$$ | (13) |
여기서, RSmodified는 수정된 형상기준이며, RSSI, RSRCCI, RSTF는 각각 SI, RCCI, TF만 이용한 형상기준이다. ai는 각 기준의 가중치이다.
2.1.3 임계값 선정
형상유사도를 바탕으로 두 객체간의 유사정도를 판단하기 위한 임계값이 필요하다. CRITIC 기법에서는 각 객체별 형상유사도 분포에서 특이점 범위에 속하는 경우의 값으로 임계값을 산정하였다. 수동으로 매칭 쌍들을 정 매칭 쌍과 오 매칭 쌍으로 구분하고 훈련자료들을 가지고 유사도를 살펴본 후 정 매칭 쌍 분포와 오 매칭 쌍 분포의 공통으로 발생하는 특이점 영역을 임계값으로 설정하였다. 본 연구는 CRITIC 기법의 형상유사도가 침수예상도와 같은 형상에 적용될 수 있는지 여부와 최적의 형상유사도 평가 방법을 도출하기 위한 연구임으로 임계값은 별도로 선정할 필요가 없다. 그러나 최적의 형상기준 방법론을 도출하기 위하여 수동으로 정 매칭쌍과 오 매칭쌍을 구분한 후 새롭게 적용된 형상기준의 적합성을 판별하였다.
2.2 연구방법론
2.2.1 적용대상
본 연구에서 사용된 참조자료는 폭풍해일에 의한 침수예상도(KHOA, 2014)이고, 유사정도를 측정하기 위한 목표자료는 SIND 모형의 결과이다. 국내의 경우 재난별로 침수예상도 등과 같은 위험예측지도를 제공하고 있다. 동해안의 위치한 도시를 대상으로 구축되어 있는 4개의 폭풍해일 침수예상도의 면 객체와 동일한 조건으로 도출한 SIND 모형결과의 면 객체의 형상유사도를 계산하였다. 각 지도별로 위험도 등급에 따라 면 객체가 구성되어 있으며, 대상 객체의 크기를 고려하여 구간을 여섯 개로 나누었다. 연구 지역 내에 존재하는 조건에 따른 등급별 총 객체 수는 175개이며 각 지도자료의 특성은 Table 1과 같다.
Table 1. Information of Maps
2.2.2 연구 방법론
Fig. 3과 같이 침수예상도와 SIND 모델 결과를 지도의 기준점을 이용하여 면 객체를 직접 중첩시켜 유사도 기반의 객체 쌍을 구축한다. 형상유사도를 도출하기 위해 각 객체의 위치, 면적, 형상의 특성을 나타내는 인자를 도출한다. 여기서, 지도의 형상특성을 반영하기 위하여 RCCI와 TF를 가중치를 이용하여 조합한 새로운 형상기준을 제안하였다. 위험지도의 최적의 형상기준을 도출하기 위한 RCCI와 TF의 조합은 수동으로 분류한 정 매칭쌍과 오매칭 쌍의 유사도 분포결과를 검토하여 도출하였다. 도출된 형상기준으로 통합 형상유사도를 도출하여 결과를 확인하였다.
새로운 형상기준을 제안하기 위하여 SI, RCCI, TF에 가중치를 주었고, 적합성 여부를 수동으로 분류된 정매칭 쌍과 오매칭 쌍의 형상유사도 분포를 통해 확인하였다. 이는 수동으로 분류한 정매칭 쌍과 오매칭 쌍이 정확하다는 것과 정매칭 쌍의 유사도 분포는 높은 값을 가지고 오매칭 쌍의 유사도 분포는 낮은 값을 가져야 한다는 전제조건이 있다.
2.2.3 SIND 모델
본 연구에서 사용된 면 객체 목표자료의 생성모델인 SIND 모델은 과학적 보간법을 활용한 재난 예측 모형이다. 기 구축되어 있는 재난 데이터베이스를 활용하여 산정한 편미분 방정식을 지배방정식으로 사용한다. 사용자가 재난별로 간단한 재난 발생조건을 입력하면 몇 초 이내로 해당 조건에 대한 위험도를 예측할 수 있다. 형상유사도 분석을 위해 사용된 대상 재난은 폭풍해일이며, 사용자가 예측하고자 하는 해일고의 빈도를 입력조건으로 한다. 모델의 결과는 해당 지역의 폭풍해일에 대한 위험도 등급별 위험지역을 도출한다(Fig. 4). 단순히 수학적 기법을 통한 모델이라는 한계를 극복하기 위하여 모델의 초기조건 및 경계조건 구성시 지역특성, 재난별 특성 등을 반영하여 재난의 물리적 특성 및 의미를 부여하였다.
2.3 적용 결과
2.3.1 정 매칭쌍(Exact Matching)과 오 매칭쌍(Mis Matching)
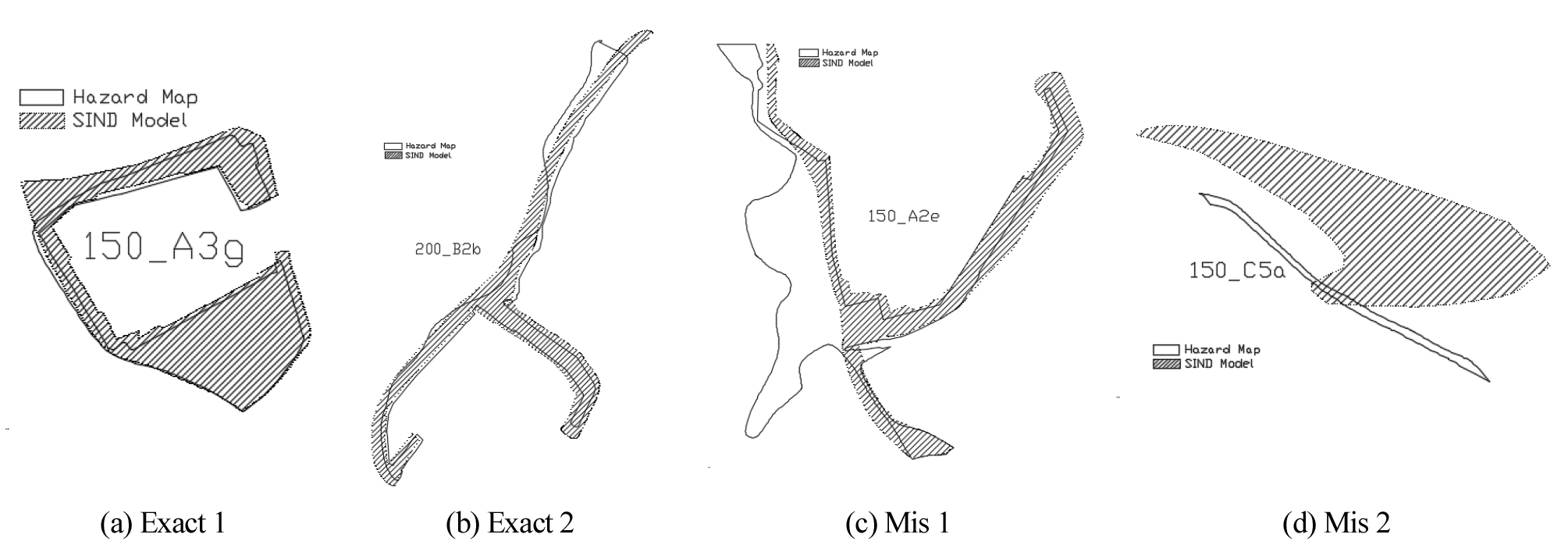
본 연구에서 최적의 형상기준을 도출하기 위해서 모든 객체 쌍을 정 매칭쌍과 오 매칭쌍으로 분류하는 작업이 필요하다. 정 매칭쌍과 오 매칭쌍의 정확한 분류가 형상기준을 도출하는데 가장 중요한 영향을 미친다. Fig. 4는 대표적인 정 매칭쌍과 오 매칭쌍을 나타낸 것이다. 이 매칭쌍을 시각적으로 살펴보면 정 매칭쌍은 형상이 유사하면서 교차되는 면적이 넓은 객체인 것을 알 수 있다. 총 175개의 매칭 쌍 중에 정 매칭 쌍은 120쌍, 오 매칭 쌍은 55쌍으로 분류되었다.
2.3.2 기준별 결과
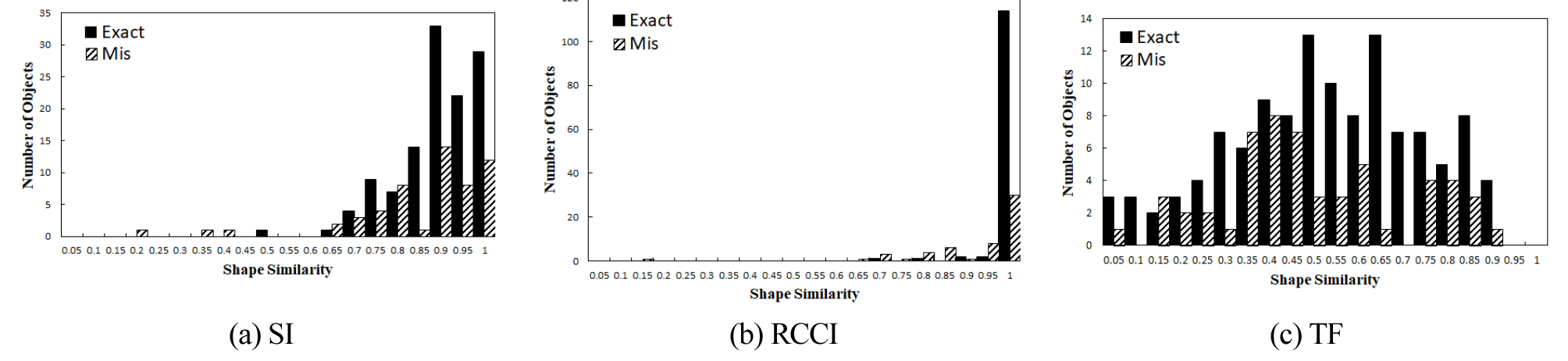
형상유사도 도출을 위해 필요한 위치기준, 면적기준, 형상기준을 계산하였다. 형상기준은 기존의 CRITIC에서 사용하는 형상지수를 통한 기준, RCCI, TF를 각각 계산하여 유사도를 도출하였다. 각 기준은 모두 0에서 1사이의 값을 가지며, 1에 가까울수록 객체가의 유사도가 높은 것을 의미한다.
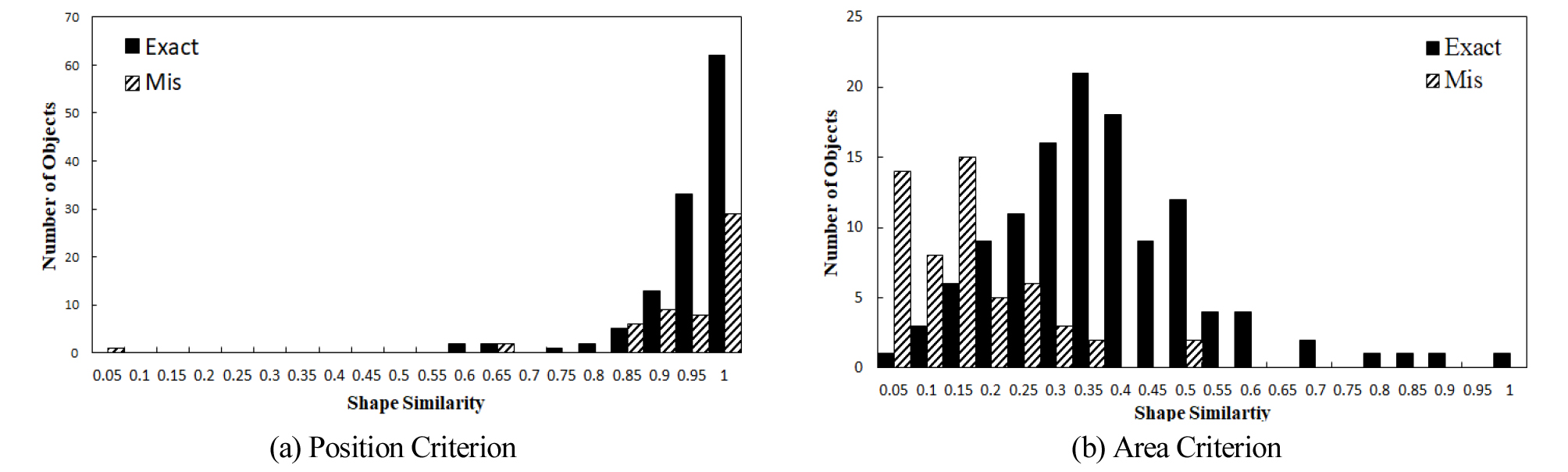
Fig. 5의 결과를 보면 위치기준은 정 매칭쌍과 오 매칭쌍 모두 유사도가 높게 나타났다. 반면에 면적기준은 전체적으로 낮은 유사도를 보였지만, 정 매칭쌍과 오 매칭쌍이 확연히 구별되는 것을 확인할 수 있었다. 각 매칭쌍의 기준별 평균값은 정 매칭쌍의 위치기준 유사도와 면적기준 유사도는 각각 0.9273, 0.3479이고, 오 매칭쌍의 경우는 각각 0.9058와 0.1399로 나타났다. 평균값 외에도 면적기준의 분포를 보면 정 매칭쌍이 오 매칭쌍보다 더 높은 유사도에 분포되어 있는 것을 알 수 있다. 이는 위험지도 객체의 종합 형상유사도는 위치기준보다 면적기준에 지배적인 것을 알 수 있다. 최적의 형상기준을 도출하기 위하여 Fig. 6과 같이 각 매칭쌍에 대하여 TF를 도출하였다. Fig. 6(b)는 Fig. 6(a)의 객체 쌍을 TF로 나타낸 것이다.
Fig. 7은 앞서 제시한 각 형상인자를 활용한 유사도 결과이다. Fig. 7(b)의 RCCI의 경우 정 매칭쌍과 오 매칭쌍을 크게 구별하지 못하는 것으로 나타났다. 예상대로 TF의 경우는 정 매칭쌍과 오 매칭쌍 모두 유사도의 분포가 다양하게 나타났다. 오 매칭쌍의 경우에도 TF를 이용한 유사도가 다수 높게 나타났는데 이는 대부분 낮은 면적기준을 가지고 있어 통합 형상유사도는 낮은 것으로 나타났다. TF는 복잡한 지형을 구현할 수 있다고 판단되지만 오 매칭쌍의 유사도가 과대산정되는 경우로 보아 TF를 형상기준의 단일지표로 사용하기엔 한계가 있다고 볼 수 있다. 따라서, 최종 형상기준은 TF와 SI를 이용하였다.
2.3.3 수정 CRITIC 기법 적용 결과
SI와 TF의 가중치를 1:9부터 9:1까지 총 9가지 경우로 형상기준을 적용하여 형상유사도를 계산하였다. 각 기준별 가중치를 변화시켜가며 정 매칭쌍과 오 매칭쌍의 형상유사도를 분석하고, 정 매칭쌍과 오 매칭쌍을 명확히 구별할 수 있는 가중치를 최적 가중치로 산정하였다. 구별근거는 각 매칭쌍의 형상유사도의 평균값의 차와 형상유사도의 분포도를 기준으로 하였다. 따라서, 상대적으로 위치기준은 정 매칭쌍과 오 매칭쌍을 구별하는데 기여도가 낮다고 판단하여 가중치를 0.1로 산정하였고, 면적기준과 형상기준은 정 매칭쌍과 오 매칭쌍의 유사도를 참고하여 가중치를 산정하였다(Table 2).
Table 2. Weights of Each Criterion
| Position Criterion | Area Criterion | Shape Criterion | |||
| a1 (SI) | a2 (RCCI) | a3 (TF) | |||
| Weights | - | - | 0.5 | 0 | 0.5 |
| w1 | w2 | w3 | |||
| 0.1 | 0.55 | 0.35 | |||
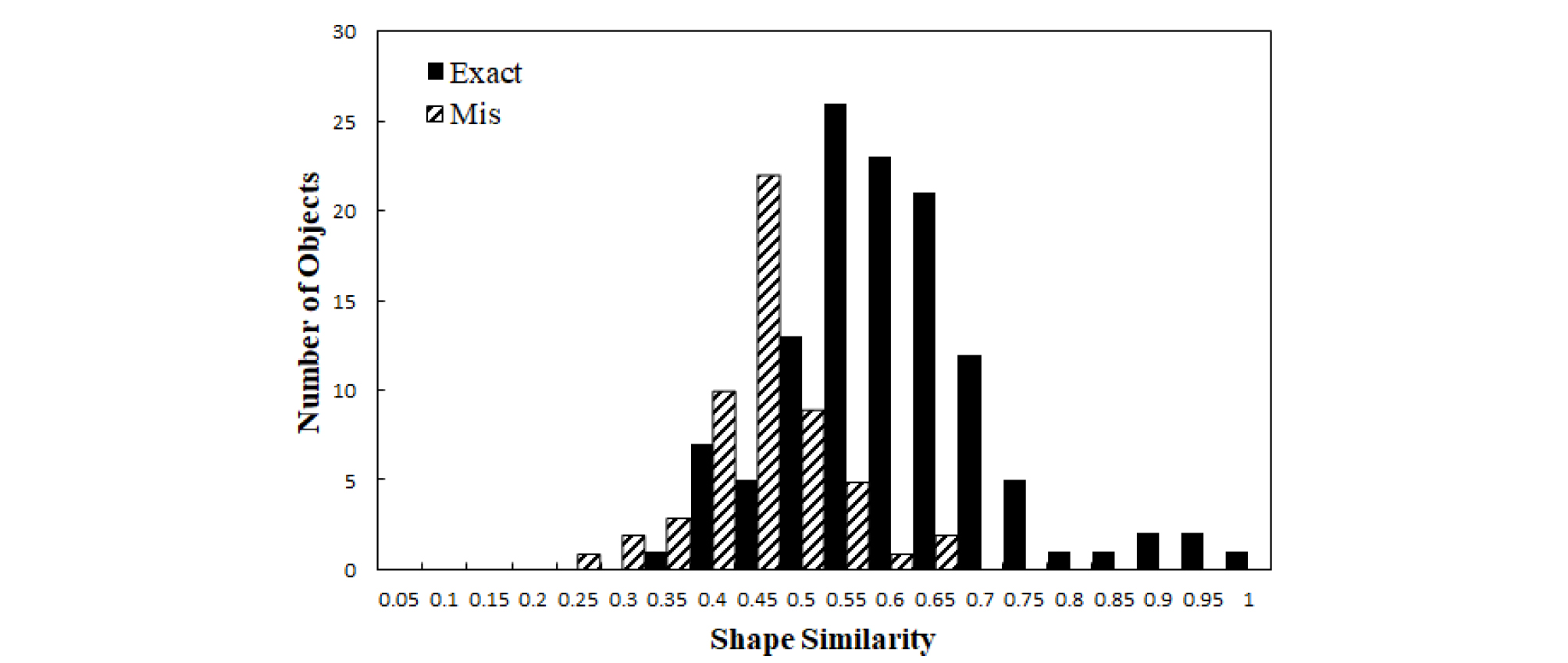
Table 2는 위험지도를 재현할 수 있는 최적의 가중치를 산정한 결과이며, 이를 이용하여 도출한 최종결과는 Fig. 8과 같다. 정 매칭 쌍의 평균 형상유사도는 0.6013이고, 오 매칭 쌍은 0.4536으로 나타났다. 형상유사도가 0.7 이상을 갖는 오 매칭쌍은 없으며, 0.5 미만의 형상유사도를 갖는 경우 총 55쌍 중 38개로 약 70%로 나타났다. 정 매칭쌍의 경우 0.7 이상을 갖는 매칭 쌍의 개수는 24개로 20%, 0.5에서 0.7 사이의 매칭 쌍은 약 70%로 나타났다. 정 매칭쌍의 경우 약 90%가 0.5 이상의 형상유사도의 값을 나타내었다. 0.5를 기준으로 분배한 결과 정 매칭쌍과 오 매칭쌍이 적절하게 분배되어 있다고 판단할 수 있다.
3. 결 론
본 연구에서는 과학적 보간 기법을 기반으로 하는 실시간 재난 위험 예측모델인 SIND 모델의 결과에 대한 적용·확대성 및 검증을 위해서 참조자료인 폭풍해일 침수예상도와 비교하는 과정에서 형상유사도의 개념을 활용하였다. 이 모델은 실시간 예측이 가능하지만 보간기법이 기반이므로, 이에 대한 정확도 검증이 필수적이다. 기존에는 정확도 검증을 위해 가장 널리 이용되는 기하학적 방법론을 토대로 만들어진 CRITIC 기법을 사용하였지만, 참조자료인 폭풍해일 침수예상도는 재난 위험도 등급별로 가늘고 긴 형태를 띄고 면 객체를 이루는 선이 복잡하게 구성되어 있기 때문에 이러한 형상적 복잡성을 반영하기 어렵다. 따라서 기존의 형상기준에 복잡한 형상을 평가할 수 있는 RCCI와 TF를 추가하였다. 객체 매칭 쌍을 정 매칭과 오 매칭으로 구분하였고 각 매칭쌍이 적합한 형상유사도를 나타낼 수 있는 형상기준 산정 방법과 가중치를 제시하였다. 총 175 매칭 쌍 중 정 매칭쌍은 120쌍, 오 매칭쌍은 55쌍으로 분류되었으며 이를 재현할 수 있는 최적 형상기준의 형상인자는 SI와 TF로 가중치를 1:1 비율로 산정하였다. 수정된 형상기준을 적용하여 형상유사도를 계산한 결과 정 매칭쌍은 약 90%가 0.5 이상의 형상유사도를 나타내었고, 오 매칭쌍의 경우 약 70%가 0.5 미만의 형상유사도를 나타내었다. 각 매칭쌍의 형상유사도의 값을 살펴보면 0.45에서 0.6 구간에 분포하는데, 위치기준의 가중치를 상향조정할 경우 형상유사도 값은 증가함을 알 수 있었다. 그러나 정 매칭쌍과 오 매칭쌍의 평균 값의 차이는 크게 변화가 없었고 이는 다수의 객체쌍이 하나의 객체쌍으로 대응되어 오 매칭쌍은 과대산정되고 정 매칭쌍은 과소 산정되는 것으로 판단된다.
따라서 향후 다수 객체와 하나의 객체쌍으로 대응되는 문제점에 대한 상세한 검토를 수행하고, 이에 따라 조정된 가중치를 적용한다면 복잡한 형상을 나타내는 지도 객체의 형상유사도 방법론을 개선할 수 있을 것이라 판단된다. 또한 형상 기준 이외에 종합 형상유사도에 영향이 큰 면적기준에 대한 추가적인 검토가 수행될 필요가 있다고 판단된다. 이후 결과를 바탕으로 유사성을 판단하는 기준인 임계값을 산정한다면 SIND 모델의 정확도를 향상시킬 수 있을 것이라 기대된다. 일반적으로 GIS 기반의 Mapping 분야에서 경험론적 방법에 의해 산정된 임계값은 약 0.70이며, 각종 피해와 직결되는 재난분야의 특성상 임계값은 0.7 이상으로 산정되어야 할 것이다.