1. 서 론
2. 적용 이론
2.1 GEV 분포
2.2 L-모멘트 법
2.3 PPCC 검정
2.4 도시 위치 공식
3. L-모멘트 법 기반의 GEV 분포 모형을 위한 PPCC 검정 통계량 유도
3.1 PPCC 검정 통계량 유도 절차
3.2 L-모멘트 법 기반의 GEV 모형을 위한 PPCC 검정 통계량 유도
3.3 회귀식 산정
4. PPCC 검정 통계량 회귀식을 이용한 기각능력 검토
4.1 모의수행조건
4.2 가정된 확률분포 모형별 기각능력 결과
4.3 연최대강우량 적용 결과
5. 결 론
1. 서 론
수문 통계학에서 확률 수문량은 가정된 확률분포 모형에 따라 크게 달라질 수 있다. 따라서 적절한 확률 수문량을 추정하기 위해서는 무엇보다 주어진 표본을 대표할 수 있는 확률분포 모형의 선정이 매우 중요하다. 또한, 추정된 확률 수문량은 수공구조물의 설계나 방재·안전 진단을 위한 값으로 활용될 수 있고 이는 곧 국민의 안전과 직결될 수 있으므로 확률분포 모형의 선정은 무엇보다 신중하게 접근해야 할 필요성이 있다. 이와 같은 중요성 때문에 수문 통계학에서는 주어진 표본에 대하여 모분포로 가정한 확률분포 모형의 적합성 여부를 판별하는 적합도 검정(goodness-of-fit test, GOF)에 대한 연구가 다양한 방법별로 꾸준히 수행되어왔다. GOF 방법에는 -검정(CS), 확률 도시 상관계수(probability plot correlation coefficient; PPCC) 검정, Anderson Darling(AD) 검정과 같은 방법들이 있다. 그 중 PPCC 검정은 정규분포에서 자료의 정규성을 알아보기 위해 Filliben(1975)에 의해 처음 제시되었다. 이 방법은 도시 위치(plotting position) 공식을 사용하여 정성적인 도시적 해석방법을 정량적으로 나타낼 수 있다는 점에서 의미하는 바가 크다고 할 수 있다(Heo et al., 2001). 또한, 기초 통계량이라고 할 수 있는 상관계수를 사용하고 있어서 이해하기 쉽고 사용하기 편리할 뿐 아니라 기각능력 또한 뛰어나다는 장점이 있다(Vogel, 1986). 이후 PPCC 검정의 간편한 사용성과 강력한 기각능력을 바탕으로 여러 연구가 지속적으로 수행됨에 따라 Gumbel과 generalized extreme value(GEV), generalized logistic(GLO), log-Pearson type III(LP3) 분포 모형 등 다양한 분포 모형에 대하여 PPCC 검정을 이용한 검정 통계량 값들이 제시되었다(Gumbel, 1958; Vogel, 1986; Vogel and McMartin, 1991; Chowdhury et al., 1991; Ahn et al., 2014). 하지만 유도된 검정 통계량 값은 표본의 크기나 확률분포 모형의 매개변수 또는 유의수준에 따라 각각 다른 값을 갖기 때문에 실무적인 적용성 측면에 다소 불편한 점이 있었다. 이에 Heo et al.(2008)은 다양한 확률분포 모형에 대해서 PPCC 검정 통계량 값을 각 모형의 매개변수와 표본의 크기를 변수로 갖는 회귀식을 유도하고 이를 유의수준별로 제시하였다.
한편, PPCC 검정 통계량을 유도하고 이를 사용하기 위해서는 확률분포 모형에 적절한 도시 위치 공식이 필수적이다. PPCC 검정은 표본 자료와 가정된 확률분포 모형에서 해당 표본 자료의 순서에 해당하는 이론적 확률 수문량의 상관성 분석을 통해 적합 여부를 판별하기 때문이다. 따라서 다양한 확률분포 모형을 위한 도시 위치 공식 연구 또한 활발히 진행되고 있다(Hazen, 1914; Kimball, 1946; Blom, 1958; Gringorten, 1963; Filliben, 1969; Cunnane, 1978; Arnell et al., 1986; In-na and Nguyen, 1989; Goel and De, 1993; Kim et al., 2012; Kim et al., 2015; Looney and Gulledge, 1985; Stedinger et al., 1993). 특히 최근에는 과거에 유도된 도시 위치 공식들과는 다르게 표본 자료의 순서 통계량뿐만 아니라 표본 자료의 왜곡도까지 고려할 수 있는 도시 위치 공식들이 개발되어 오고 있다(In-na and Nguyen, 1989; Goel and De, 1993; Kim et al., 2012; Kim et al., 2015). 그 중, Kim et al.(2012)와 Kim et al.(2015)는 표본 자료의 왜곡도 계수를 고려할 수 있는 도시 위치 공식을 각각 GEV와 GLO 모형에 대해 제시하였으며 제시된 새로운 도시 위치 공식은 기존의 다른 도시 위치 공식보다 더 낮은 오차와 높은 결정계수를 보이는 것으로 확인되었다. Ahn et al.(2014)는 Kim et al.(2012)가 제시한 도시 위치 공식을 활용하여 새로운 PPCC 검정 통계량을 유도하고 사용 편의성을 고려하여 회귀식을 제시하였다. 또한, Monte Carlo 모의실험(MCS)을 통해 기존의 도시 위치 공식을 활용한 PPCC 검정 방법과의 비교 분석 결과 더 높은 기각능력을 보이는 것을 확인하였다.
하지만 확률분포 모형을 추정할 때 모형의 매개변수 추정방법에 따라 추정된 모형은 다를 수 있으며, 이는 서로 다른 확률 수문량을 추정할 수 있다는 것을 의미한다. Ahn et al.(2014)의 경우 모멘트 법을 기반으로 하여 검정 통계량을 추정하였기 때문에 다른 매개변수 추정방법에 따라 추정된 모형에 적용은 어려울 수 있다. 따라서 본 연구에서는 모멘트 법보다 편의(bias) 측면에 더 안정적이고 다양한 극치 자료 분석 및 지역 빈도해석에서 널리 이용되고 있는 L-모멘트 법 기반의 매개변수 추정 기법을 활용하여 GEV 분포 모형을 위한 PPCC 검정 통계량을 유도하고 사용 편의성을 위하여 이를 회귀식 형태로 간단히 제시하고자 한다.
2. 적용 이론
2.1 GEV 분포
GEV 분포 모형은 극치 수문 사상 해석 분야에서 주로 이용되고 있으며, 우리나라에서 관측되는 극치 수문 자료에 대해서도 Gumbel 분포 모형과 함께 가장 적절하다고 알려져 있다(Heo et al., 1999; KICT, 2000). GEV 분포 모형은 3개의 매개변수를 가지고 있는 확률분포 모형으로서 2변수 확률분포 모형인 Gumbel 분포 모형과 비교하면 상대적으로 적용성이 좋으며, 매개변수의 조건에 따라 Gumbel 분포 모형을 나타낼 수 있다. GEV 분포의 누적분포함수(cumulative distribution function, CDF)는 다음과 같다(Jenkinson, 1955).
| $$F(x)=exp\lbrack-exp\{{-(x-x_0)/\alpha\}}\rbrack,\;\;\;\;\;\;\;\;\beta=0$$ | (1a) |
| $$\;\;\;\;\;\;\;\;=exp\lbrack-\{{1-\beta(x-x_0)/\alpha\}}^{1/\beta}\rbrack,\;\;\;\;\beta\neq0$$ | (1b) |
여기서, , , 는 각각 위치(location), 규모(scale), 형상(shape) 매개변수를 나타내고, 형상 매개변수 가 0일 경우 Gumbel 분포, 음수일 경우 Fréchet 분포, 양수일 경우는 Weibull 분포를 나타낸다.
2.2 L-모멘트 법
L-모멘트 법은 모멘트 차수가 다른 몇 개의 확률 가중 모멘트를 선형 조합함으로써 일반적인 모멘트 법에 비해 편의를 제거하고자 제시된 방법이다(Hosking, 1990). 일반적인 모멘트 법의 경우 표본 크기가 작은 경우 변동 계수나 왜곡도 계수와 같은 값들이 크게 편의 되는 경향이 있지만, L-모멘트 법의 경우에는 거의 편의 되지 않기 때문이다. 또한, 표본 L-모멘트 비(sample L-moment ratio)를 이용하여 다양한 수문 자료의 특성을 도시적으로 나타낼 수 있기 때문에 널리 이용되고 있다. GEV 분포 모형의 매개변수 추정을 위하여 L-모멘트 법 이용을 위한 확률 가중 모멘트의 선형조합과 공식은 Hosking(1990)이 제시한 방법을 참고하였다.
2.3 PPCC 검정
PPCC 검정은 두 자료 간의 상관성 관계를 바탕으로 GOF 방법을 수행하는 방식이다. 여기서 말하는 두 자료는 관측 및 수집으로 취득된 자료를 순차적으로 정렬한 자료와 모분포로써 가정된 확률분포 모형으로부터 생성되는 자료를 순차 정렬한 자료를 의미한다. 이때의 상관성 관계 측정은 Eq. (2)와 같은 적모멘트 상관계수를 이용한다.
| $$r_c=\frac{\displaystyle\sum_{i=1}^n\left(X_i-\overline X\right)\left(M_i-\overline M\right)}{\sqrt{\displaystyle\sum_{i=1}^n{(X_i-\overline X)}^2\sum_{i=1}^n{(M_i-\overline M)}^2}}$$ | (2) |
여기서, 는 관측되거나 수집된 표본 자료이고, 이고, 는 참값으로 가정된 확률분포 모형의 CDF의 역함수를 의미하고 는 가정된 확률분포 모형을 대표할 수 있는 도시 위치 공식으로부터 산정된 누적확률을 의미한다.
2.4 도시 위치 공식
도시 위치 공식은 수집된 표본 자료가 순서 통계량을 통해서 이론적 분포형으로부터 각각 어떠한 누적확률을 갖는지 알 수 있는 방법으로 다양한 분야에서 널리 이용되고 있다. 특히 수문 분야에서는 GOF나 특정 수문량에 대한 비초과확률 및 초과확률을 산정하기 위한 확률도시법(probability plotting technique)등에 널리 이용되고 있다. 특히 PPCC 검정에서는 확률분포 모형과 그 확률분포 모형이 갖는 형상 매개변수에 따라 PPCC 검정 통계량 값이 달라지기 때문에 분포형별로 적절한 누적확률을 산정해주는 도시 위치 공식의 선정이 중요하다(Ahn et al., 2014). 본 연구에서는 표본 자료의 왜곡도를 고려할 수 있으며 GEV 분포 모형에 가장 적절하다고 알려진 도시 위치 공식을 활용하였다(Kim et al., 2012). 적용된 도시 위치 공식은 Eq. (3)과 같다.
| $$P_i=\frac{i-0.3200}{n+0.0149\gamma^2-0.1364\gamma+0.3225}$$ | (3) |
여기서, 는 표본 자료의 오름차순 순서, 은 표본 크기, 는 표본 자료의 왜곡도 계수를 의미한다. 왜곡도 계수는 또 다른 표현으로 비대칭도 또는 왜도라고 사용될 수 있으며 정량적인 기술 통계적으로는 3차 표준 모멘트로 정의할 수 있다. 표본 자료의 왜곡도 계수가 음수일 경우 확률밀도함수에서 왼쪽 꼬리 부분이 긴 꼬리 형태를 취하고, 반대로 양수일 경우 확률밀도함수의 오른쪽 꼬리 부분이 긴 꼬리 형태를 취한다. 이러한 왜곡도 계수는 확률분포 모형의 형상 매개변수와 아주 밀접한 관계가 있다고 알려져 있다(Kim et al., 2012). 본 연구에서 적용된 도시 위치 공식은 GEV 분포 모형의 형상 매개변수 –0.2에서 +0.2 범위 내에서 적절한 것으로 알려져 있다(Kim et al., 2012).
3. L-모멘트 법 기반의 GEV 분포 모형을 위한 PPCC 검정 통계량 유도
앞서 2.3 PPCC 검정에서 설명하였듯이 PPCC 검정은 실제 관측자료로부터 얻은 표본과 이론적 분포형으로부터 얻은 확률 수문량 값과의 선형적 상관성을 통해서 GOF를 수행하게 된다. 일반적으로 이론적 분포형의 확률 수문량 값은 CDF의 역함수에 누적 발생확률값을 대입함으로써 구할 수 있는데, 이때 CDF의 역함수에 대입하는 확률값은 도시 위치 공식을 통해 산정하게 된다. 결국, PPCC 검정은 확률분포 모형에 대한 적절한 도시 위치 공식에 따라 그 기각능력이 좌우된다고 볼 수 있다. 따라서 본 연구에서는 PPCC 검정 통계량을 유도하기 위해 표본 자료의 왜곡도를 고려할 수 있을 뿐만 아니라 GEV 분포 모형에 적합하다고 알려진 도시 위치 공식을 적용하였다. 또한, L-모멘트 법을 이용하여 GEV 분포 모형의 매개변수 추정하였다. 마지막으로 MCS를 통해 PPCC 검정 통계량을 유도하고 이를 회귀식으로 제시하였다.
3.1 PPCC 검정 통계량 유도 절차
Vogel and McMartin(1991)은 MCS를 이용한 PPCC 검정 통계량 유도 방법을 다음과 같이 제시하였다.
①확률분포 모형의 매개변수와 표본 크기별 자료를 100,000개씩 발생시킨다(이때 크기와 규모 매개변수는 각각 0과 1로 고정).
②유도하고자 하는 확률분포 모형에 적절한 도시 위치 공식을 적용하여 누적확률을 구한 뒤, CDF의 역함수를 이용하여 이론적 확률 수문량을 구한다.
③①번 과정에서 발생시킨 자료와 ②번 과정에서 구한 이론적 확률 수문량 Eq. (2)을 통해서 PPCC 검정 통계량 을 산정한다.
④이때 유의수준 에 대한 는 중에서 100,000×번째로 작은 값과 같고 Eq. (4)와 같이 표시할 수 있다.
| $$r_\alpha=r_{(100,000\alpha)}$$ | (4) |
이때, 는 확률분포 모형의 형상 매개변수, 표본 크기 그리고 유의수준에 따라 각각 다른 값을 가진다.
3.2 L-모멘트 법 기반의 GEV 모형을 위한 PPCC 검정 통계량 유도
GEV 분포 모형에서 PPCC 검정 통계량을 유도하기 위하여 생성된 표본 자료에 대해 L-모멘트 법을 활용하여 GEV 분포 모형의 매개변수를 추정하였다. 모의 발생 시 사용된 표본 크기는 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200, 300으로 총 13가지의 경우로 나누었고, 형상 매개변수는 –0.20부터 +0.20까지 0.05 간격으로(0.00 제외) 8개의 범위를 사용하였으며, 형상 매개변수와 표본 크기에 따라 각각 100,000개의 표본 자료를 발생시켰다. 검정 통계량 유도 방법은 3.1 PPCC 검정 통계량 유도 절차에서 언급된 Vogel and McMartin(1991)이 제시한 방법을 참고하였다. 모의 발생으로 생성된 표본 자료의 비초과 확률을 추정하기 위하여 사용된 도시 위치 공식은 GEV 분포형에 가장 적합한 것으로 알려져 있으며 표본 자료의 왜곡도 계수를 고려할 수 있는 Kim et al.(2012)이 제시한 Eq. (3) 방법을 이용하였다. 유의수준은 1%, 5%, 10%, 그리고 15%에 대하여 검정 통계량을 산정하였다.
3.3 회귀식 산정
PPCC 검정 통계량은 표본 크기, 형상 매개변수 및 유의수준에 따라 각각 다르므로 이를 사용하기 간편하도록 하나의 회귀식으로 표현할 수 있도록 유도하였다. 회귀식의 형태는 Heo et al.(2008)이 제시한 식의 형태를 참고하였다. 앞서 유도된 회귀식은 =0.01일 경우를 제외하고 GEV 분포 모형에서 형상 매개변수 –0.20에서 +0.20까지 사용할 수 있다. =0.01일 때 –0.20에서 –0.15까지의 범위에 해당하는 PPCC 검정 통계량은 Heo et al.(2008)이 제시한 식의 형태를 따르지 않기 때문에 제외하였다. 본 연구에서 사용한 회귀식 형태와 유의수준에 따른 사용 가능한 GEV 분포 모형의 형상 매개변수의 범위는 Eq. (5)와 같다. Eq. (5)의 유의수준별 매개변수는 Table 1과 같다.
| $$\ln\left(\frac1{1-r_\alpha}\right)=(a_1+a_2\beta+a_3\beta^2+a_4\beta^3)\cdot n^{(a_5+a_6\beta+a_7\beta^2)}$$ | (5) |
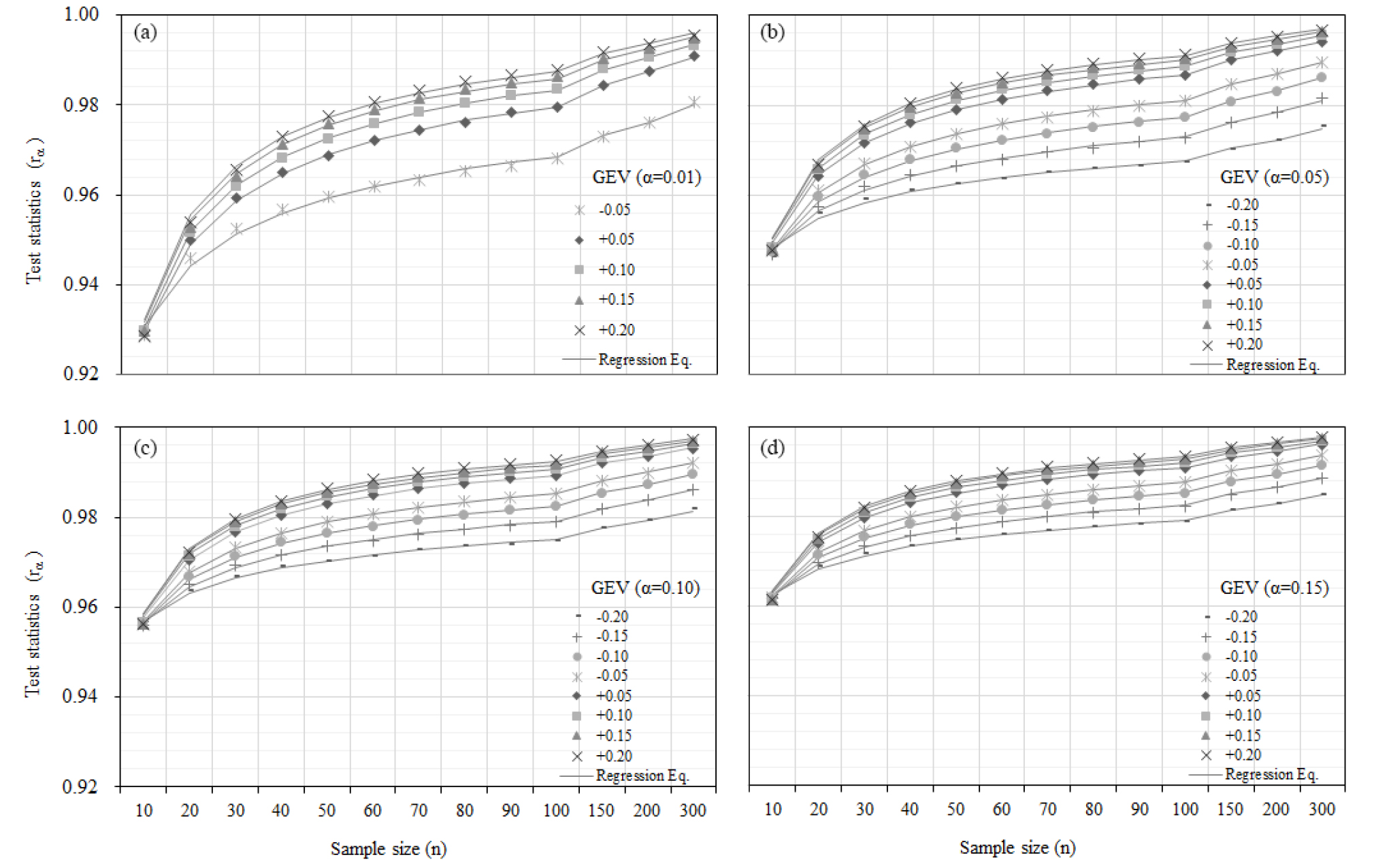
여기서, 는 유의수준 일 때 PPCC 검정 통계량, 는 GEV 분포 모형의 형상 매개변수, 그리고 은 표본 크기를 의미한다. 유도된 PPCC 검정 통계량과 이를 회귀식으로 나타낸 결과는 Fig. 1과 같다. Fig. 1(a)는 유의수준 0.01일 때의 GEV 분포 모형에 대한 PPCC 검정 통계량과 회귀식을 나타낸 것이다. Fig. 1(b)는 유의수준 0.05, Fig. 1(c)는 유의수준 0.10, 그리고 Fig. 1(d)는 유의수준 0.15일 때의 결과값을 나타낸다.
Table 1. Parameters of regression equation for each plotting position formula
본 연구에서 제시된 회귀식이 유도된 검정 통계량 값을 얼마나 잘 나타내는지에 대하여 상관계수와 결정계수(coefficient of determination, )로써 검증하였다. 가장 낮은 상관계수와 결정계수는 유의수준 0.05일 때 GEV 분포 모형의 형상 매개변수–0.20일 때 나타났으며 그 값은 각각 0.9964와 0.9925이다. 가장 낮은 상관계수와 결정계수가 0.99 이상의 결과값을 가짐으로 본 연구에서 제시된 회귀식이 유도된 검정 통계량을 잘 나타내고 있음을 확인하였다. 각 유의수준별 GEV 모형에 대한 PPCC 검정 통계량에 대한 회귀식의 상관계수와 결정계수는 Table 2와 같다.
Table 2. and correlation coefficient of regression equation
4. PPCC 검정 통계량 회귀식을 이용한 기각능력 검토
본 연구에서 제시된 PPCC 검정 통계량 회귀식(PPCC-A)의 기각능력 검토를 위하여 MCS를 수행하였다. 여기서 기각능력의 정의는 GEV 분포 모형이 아닌 다른 확률분포 모형으로부터 생성된 표본을 GEV 분포 모형이 아니라고 찾아내는 것을 의미하며, 다른 확률분포 모형으로부터 생성된 표본의 횟수와 각 검정 방법으로부터 나온 기각 능력의 비율로 나타내었다. 기각능력의 비교 검증을 위해 -검정, Cunnane(1978)이 제시한 도시 위치 공식을 이용한 PPCC 검정(PPCC-C), 그리고 기존 AD 검정을 개선한 modified AD 검정(MAD)을 함께 적용하였다. MCS를 위하여 총 4가지의 모분포 모형(population model)을 사용하였고, 그중 형상 매개변수를 갖는 분포형은 각각 8가지의 형상 매개변수를 고려하였으며 분포형별로 7가지의 표본 크기로 5,000번씩 반복하여 발생시켰다.
4.1 모의수행조건
MCS를 위한 적용 모분포 모형은 왜곡된 분포 모형(skewed distribution model)과 좌우 대칭인 분포 모형(symmetric distribution model)으로 나누어 각각 2개씩 총 4개의 분포 모형을 이용하였다. 대칭인 분포형으로는 normal과 logistic 분포 모형을 이용하였고 왜곡된 분포형으로는 GEV와 GLO 분포 모형을 이용하였다. 그 중 왜곡된 분포형은 각 분포 모형별로 0.25에서 3.60까지의 왜곡도 계수에 해당하는 8가지의 형상 매개변수를 사용하였다. 표본 크기는 10, 20, 30, 40, 50, 80, 100으로 총 7가지의 경우를 고려하였다. 이를 바탕으로 분포형에 따라 형상 매개변수와 표본 크기 별로 각각 5,000번씩 반복 수행한 뒤 GOF(유의수준 5%)를 수행하였다. 기각능력 검토를 위한 MCS 조건을 정리한 내용은 Table 3와 같다.
Table 3. Conditions of power test
4.2 가정된 확률분포 모형별 기각능력 결과
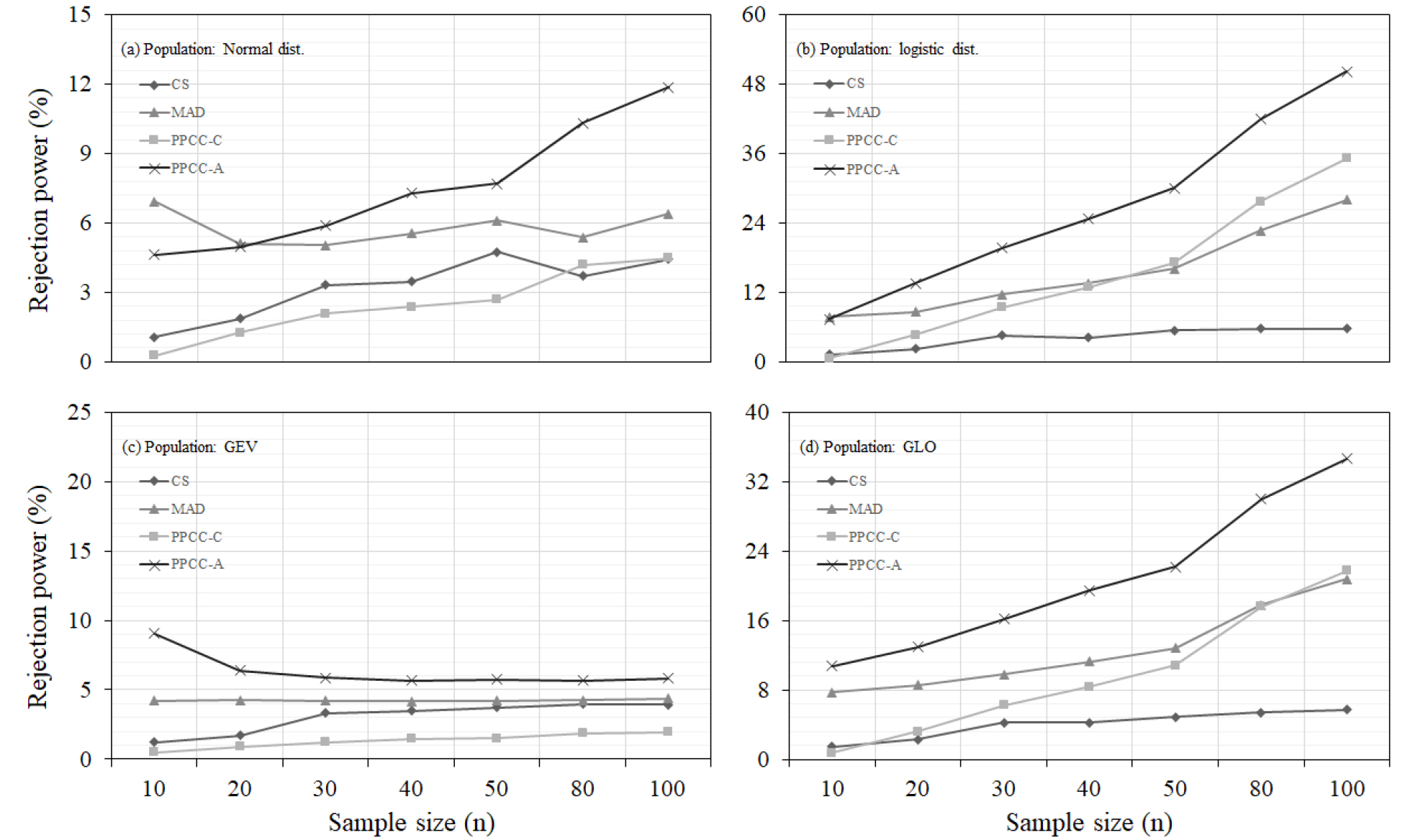
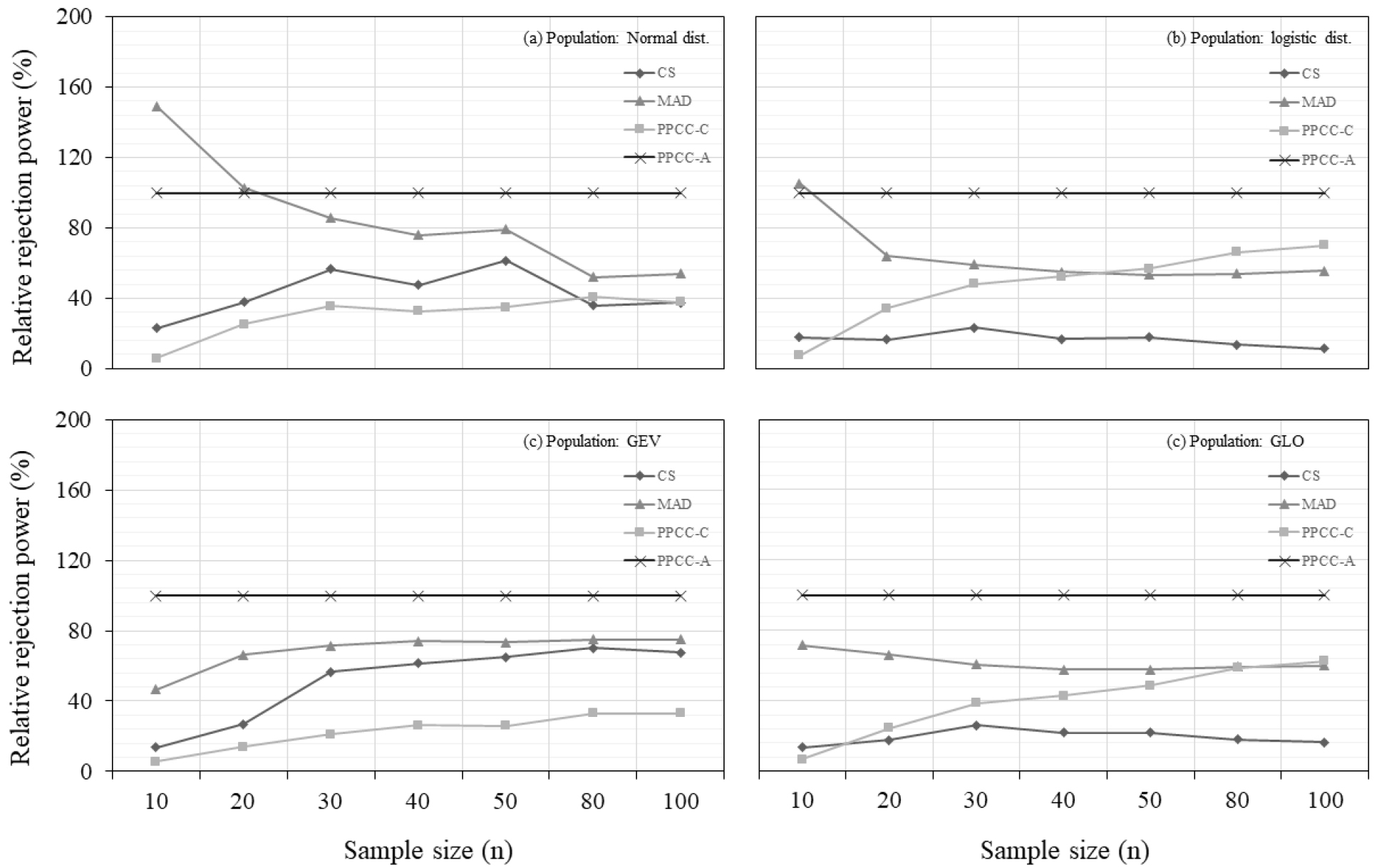
Table 3에 정리된 조건을 바탕으로 MCS를 이용한 GOF 방법별 기각능력 비교 결과는 Fig. 2와 같다. Fig. 2(a)는 모분포 모형으로 Normal 분포 모형을 이용하여 MCS를 수행한 결과이다. 표본 크기가 10일 경우를 제외하고 본 연구에서 새롭게 제시된 PPCC-A 방법이 가장 높은 기각력을 보여주고 있고 그 다음으로는 MAD, CS, PPCC-C 순으로 기각력이 높았다. Fig. 2(b)는 logistic 분포 모형을 이용하여 MCS를 수행한 결과이다. 전체적으로 표본 크기가 증가함에 따라 검정 방법에 관계없이 기각력이 증가하는 것이 확인되었다. Fig. 2(a)에서와 마찬가지로 PPCC-A가 가장 높은 기각력을 보여주었다. 그 다음으로는 PPCC-C와 MAD가 높은 기각력을 보였다. 다만 표본 크기 50을 기준으로 표본 크기 50보다 작은 영역에서는 MAD의 기각력이 높았고 그보다 큰 영역에서는 PPCC-C가 높은 기각력을 보였다. Fig. 2(c)의 경우는 모분포 모형을 GEV로 하여 MCS를 통한 기각능력을 검증한 결과이다. GOF 방법에 관계없이 표본 크기가 커짐에 따라 유의수준 5%에 수렴하는 모습을 확인할 수 있었다. 다만 PPCC-A의 경우 표본 크기 10에서 상대적으로 다른 GOF 방법들보다 높은 기각력을 보여주었다. PPCC-C의 경우도 표본 크기가 증가함에 따라 유의수준에 수렴하는 양상을 보이긴 하였으나 상대적으로 다른 GOF에 비해 유의수준 5%에 수렴하는 정도가 낮았다. 마지막으로 Fig. 2(d)에서는 모분포 모형을 GLO로 하여 MCS를 수행한 결과이다. 이전 결과들과 마찬가지로 표본 크기가 커짐에 따라 기각능력이 향상됨을 확인하였고, PPCC-A가 가장 높은 기각력을 보여주었다. Fig. 2(b)에서의 결과와 마찬가지로 MAD와 PPCC-C는 표본 크기 80을 기준으로 기각력의 차이를 보였다. 모분포 모형의 형태(대칭, 왜곡)와 종류와 관계없이 표본 크기가 증가함에 따라 각각의 GOF 방법별로 기각력이 증가하는 것을 확인할 수 있었고 본 연구에서 제시된 PPCC-A의 기각력이 가장 높은 것을 확인할 수 있었다. 특히 기존에 표본 자료의 순서 통계량만을 고려한 도시 위치 공식을 사용한 PPCC-C 검정 방법보다 새롭게 적용된 PPCC-A 검정 방법이 향상된 기각력을 가지고 있음을 확인하였다. Fig. 3은 전체적으로 높은 기각력을 보여준 PPCC-A 검정의 기각력을 기준으로 다른 검정 방법들의 상대적 기각력을 나타낸 결과이다. Fig. 3(a)와 Fig. 3(b)에서 표본 크기 10일 때를 제외한 모든 영역에서 PPCC-A가 다른 검정 방법들보다 높은 기각력을 보이는 것을 확인할 수 있었다.
4.3 연최대강우량 적용 결과
앞 절에서의 모의실험 결과 검증 및 본 연구에서 새롭게 유도된 적합도 검정의 실제 자료에 대한 적용성을 검토하기 위하여 기상청 관측 지점 중 마산(155), 순천(174), 부안(243), 거제(294)를 대상으로 지속기간 1시간에 해당하는 연최대강우량 자료에 PPCC-C와 PPCC-A을 적용하여 적합도 검정을 수행하였다. 주어진 표본 데이터를 대상으로 GEV 분포 모형을 대상 모형으로 L-모멘트 법을 적용하여 매개변수를 추정하였다. 적용 결과는 Table 4와 같다. 적용 대상지점 4곳은 왜곡도 계수가 0.54에서 2.39까지 다양하게 나타났다. GEV 분포 모형의 PPCC-C를 이용한 결과는 모두 통과로 나왔지만 PPCC-A를 이용한 적합도 검정 결과는 모두 기각으로 나타났다. 이를 통해 본 연구에서 새롭게 유도된 방법이 기존의 PPCC 검정 방법 보다 기각능력이 우수해진 것을 확인할 수 있었으며 다양한 왜곡도 계수와 이에 상응하는 형상 매개변수에서 적용이 가능한 것으로 확인되었다.
Table 4. Summary of the PPCC tests (Masan, Suncheon, Buan, Geoje)
5. 결 론
본 연구에서는 L-모멘트 법 기반의 GEV 분포 모형을 위한 PPCC 검정 통계량을 유도하고 새롭게 제시된 방법의 기각력 검토를 위해 모의실험을 수행하였다. 이를 위해서 표본 자료의 순서 통계량뿐만 아니라 왜곡도를 고려할 수 있는 도시 위치 공식을 적용하였다. 다양한 표본 크기, GEV 분포 모형의 형상 매개변수, 그리고 유의수준에 따른 각각의 검정 통계량을 간편하게 이용할 수 있도록 하나의 통합된 다변량 비선형 형태의 회귀식으로 나타내었다. 회귀식의 검증은 상관계수와 결정계수로 평가하였으며 각각 0.99 이상의 값으로 유도된 검정 통계량 값을 잘 나타내어 주고 있음을 확인하였다. 본 연구에서 새롭게 제시된 PPCC-A 검정의 기각력 검토를 위해서 다양한 GOF 방법들과 함께 여러 가지 조건에서 MCS를 수행하였다. 그 결과 PPCC-A가 기존의 PPCC를 비롯한 다른 GOF 방법들보다 개선된 기각력을 보여주는 것으로 확인되었다. 또한, 모의실험의 결과를 바탕으로 실제 수문자료의 적용성 검토를 수행하기 위하여 지속기간 1시간에 해당하는 연최대 강우자료에 대하여 다양한 왜곡도 계수를 갖는 지점을 대상으로 PPCC-C 방법과 PPCC-A 방법을 적용시켜 결과를 분석해 보았다. 분석 결과 새롭게 제시된 PPCC-A 방법의 경우 다양한 왜곡도 계수의 범위에서 적용이 가능한 것으로 분석되었으며, 기존의 방법보다 기각능력이 향상되었음을 확인할 수 있었다. 이를 통해서 본 연구에서 새롭게 제시된 GOF 방법을 통해서 기존 GOF 방법들이 가지고 있는 한계를 개선하고 표본 자료에 대해 좀 더 정확한 확률분포 모형을 추정하는 데 있어서 기여할 수 있을 것으로 기대된다.